Derivatives through first principle rule (Ab-initio method)

If you need to hire services for language tutoring, website designing, logo making, video animation, search engine optimization, and much more, then please click the following links, you’ll find qualitative and reliable services at reasonable rates;

Please watch: "Limit of a function f(x): Epsilon ϵ and Delta δ definition with example"

"DERIVATIVES THROUGH FIRST PRINCIPLE RULE (AB-INITION METHOD):-
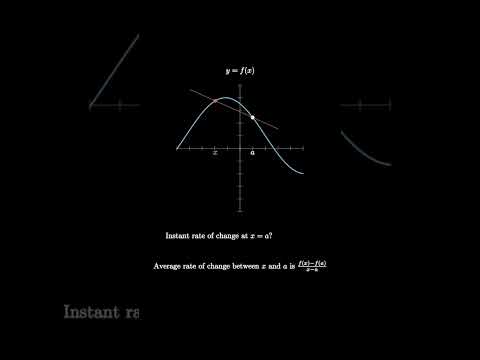
As we noticed in the geometrical interpretation of differentiation, we can find the derivative of a function at a given point. If the derivative exists for every point of the function, then it is defined as the derivative of the function f x.
Suppose f x is a real valued function, the function defined by
limit 'h' tending to '0' f x+h - f x / h
For this function, if the derivative exists at every point along the curve, then we say
f'(x) = limit 'h' tending to '0' f x+h - f x / h
This definition of derivative of f x is called the First Principle of Derivatives.
The function f' x or dy/dx is called the gradient function.
The process of finding the gradient value of a function at any point on the curve is called differentiation, and the gradient function is called the derivative of f x.

"Tangent line and derivatives"