filmov
tv
Infinitely Nested Michael Jordans

Показать описание
Infinitely Nested Square Roots,
sqrt(20+sqrt(20+sqrt(20+...))),
⭐️Please subscribe for more math content!
Check out my site & social media
Thank you for supporting! You're awesome and I know it!
blackpenredpen | 曹老師
sqrt(20+sqrt(20+sqrt(20+...))),
⭐️Please subscribe for more math content!
Check out my site & social media
Thank you for supporting! You're awesome and I know it!
blackpenredpen | 曹老師
Infinitely Nested Michael Jordans
A super fast math trick for nested square roots
A nice nested radical problem!!
Dear Tejas, challenge ACCOMPLISHED! (Speed run, Uncut)
How to get Ramanujan's Infinite Nested Radical, √(1+2√(1+3√(1+4√(1+5√(1+...))))), from Scratch....
Can you solve these infinitely nested square roots of i? #shorts
An awesome infinitely nested radical.
Integrating Infinitely Nested Square Roots
Infinitely Nested Square Roots
Spicing up SyberMath's nested radical equation with an infinitly nested one and a bonus integra...
nested square roots
x=5 as an infinity nested square root
a nested square root!
sqrt(0+sqrt(0+sqrt(0+...))) = ?
Grade 9: Solving Infinitely Nested Radicals
Solving An Infinite Radical for x
How to solve infinite nested radicals
Interesting trick to solve an interesting problem on infinite nested radical
Infinitely Nested Radicals
This Magic Trick Explained 😯
Infinitely Nested Integral Problem
An infinite nested radical series || Interesting problem to solve
Derivative and Integral of two Infinitely Nested Radicals - Inspired by MIT Integration Bee
Special Nested Root (Part 1)
Комментарии
 0:11:34
0:11:34
 0:00:20
0:00:20
 0:21:22
0:21:22
 0:04:24
0:04:24
 0:06:50
0:06:50
 0:00:26
0:00:26
 0:13:27
0:13:27
 0:03:04
0:03:04
 0:07:34
0:07:34
 0:06:47
0:06:47
 0:00:27
0:00:27
 0:00:55
0:00:55
 0:00:16
0:00:16
 0:07:56
0:07:56
 0:04:53
0:04:53
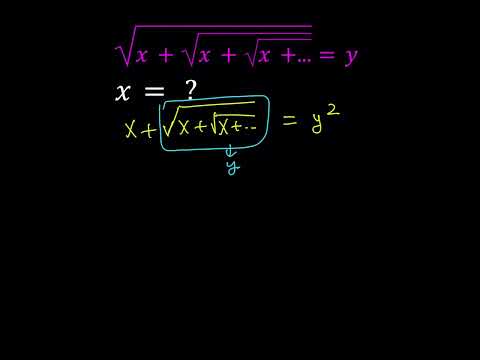 0:00:38
0:00:38
 0:02:20
0:02:20
 0:03:42
0:03:42
 0:15:05
0:15:05
 0:00:28
0:00:28
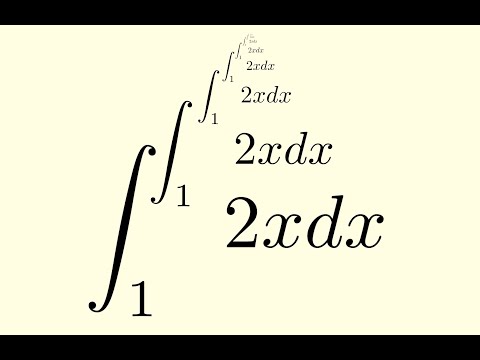 0:10:09
0:10:09
 0:03:02
0:03:02
 0:10:22
0:10:22
 0:07:25
0:07:25