filmov
tv
Infinitely Nested Integral Problem
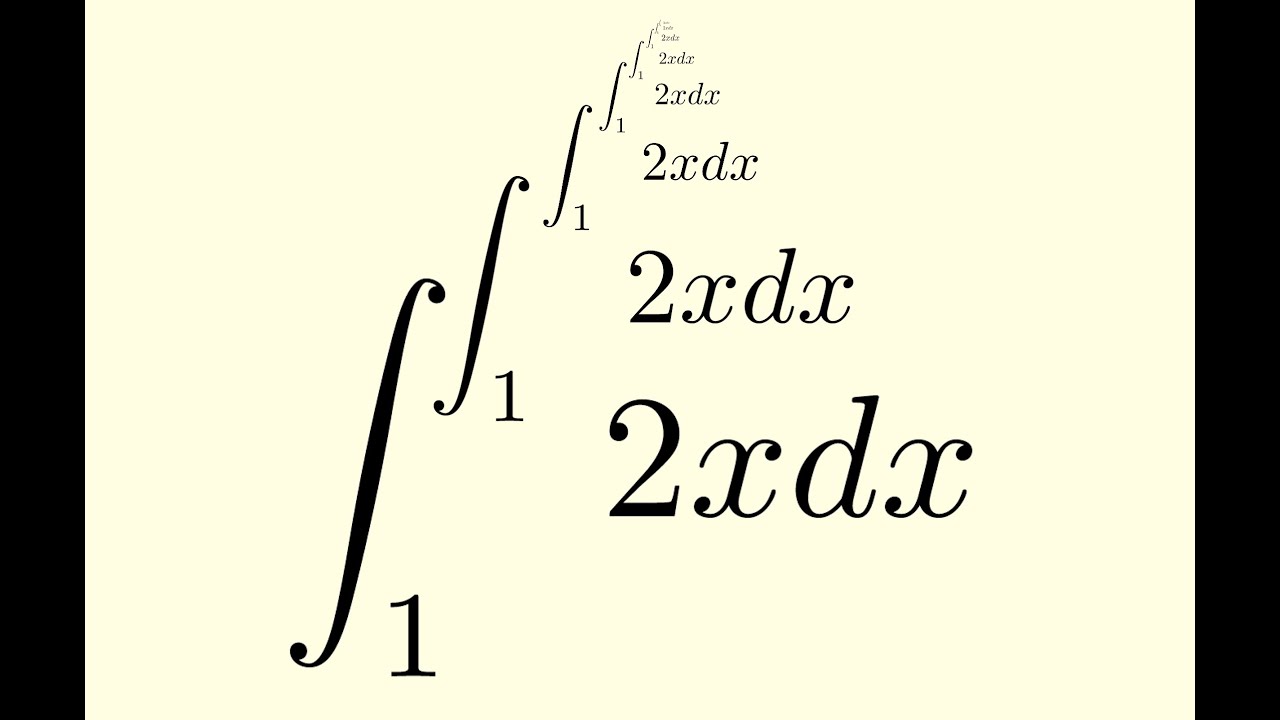
Показать описание
We solve a fun infinitely nested integral problem. Posing the problem in a more rigorous way leads to an interesting discussion of fixed-point iteration.
00:00 What does it mean?
00:30 A neat solution
02:15 More rigorous approach
04:37 A solution using iteration
06:37 More solutions?
00:00 What does it mean?
00:30 A neat solution
02:15 More rigorous approach
04:37 A solution using iteration
06:37 More solutions?
Infinitely Nested Integral Problem
Integrating infinite nested sines
Surprising Infinite Nested Integral
A crazy infinitely nested sine integral from the 2022 MIT Integration Bee Qualifying Exam
This Infinite Integral Tower Actually Converges? Sorta...
Integrating Infinitely Nested Square Roots
Derivative and Integral of two Infinitely Nested Radicals - Inspired by MIT Integration Bee
Integral of a Infinitely Nested Radical
Infinite Improper Integrals, Quiz 3 Problem 1
Quite Interesting... A Nested Infinite Logarithmic Integral!
Infinite Nested Quintic Sum
Integral of Infinite Nested Exponents of Sine and Cosine functions
Improper Integrals - Convergence and Divergence - Calculus 2
Evaluating Improper Integrals
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Infinitely Nested Radical!!! What do we do now???
Hard Viral Integration Problem | Nested infinite square root problem |Indefinite Integral.
Two Infinite Sums Inside a Putnam Integral
Infinitely Nested Michael Jordans
Derivative of an infinitely nested radical
Insane Math,The Infinite Sin(x) Root Challenge
√(6 + √(6 + √(6 + √(…)))). Solving sum of infinite radical equation
A super fast math trick for nested square roots
How to do two (or more) integrals with just one
Комментарии
 0:10:09
0:10:09
 0:11:17
0:11:17
 0:05:50
0:05:50
 0:06:56
0:06:56
 0:13:08
0:13:08
 0:03:04
0:03:04
 0:10:22
0:10:22
 0:02:15
0:02:15
 0:11:29
0:11:29
 0:10:50
0:10:50
 0:25:15
0:25:15
 0:06:27
0:06:27
 0:13:56
0:13:56
 0:12:24
0:12:24
 0:00:09
0:00:09
 0:05:17
0:05:17
 0:05:27
0:05:27
 0:24:35
0:24:35
 0:11:34
0:11:34
 0:01:32
0:01:32
 0:00:36
0:00:36
 0:00:59
0:00:59
 0:00:20
0:00:20
 0:18:03
0:18:03