filmov
tv
Calculate the angle alpha | Learn 3 Strategies for Finding Missing Angles

Показать описание
In this lesson, we calculated the missing angle in the given triangle in three different ways. During our calculations, we utilized properties of isosceles triangles, similar triangles, and the law of sines. Please watch the video until the end to learn these methods.
Don't forget to subscribe and turn on the notification bell! :)
Thank you for watching.
#math#maths#geometrypuzzle
Don't forget to subscribe and turn on the notification bell! :)
Thank you for watching.
#math#maths#geometrypuzzle
Finding The Angle Alpha
Calculate the angle alpha | Learn 3 Strategies for Finding Missing Angles
Two Methods Without Trigonometry: Find Angle alpha
Determine angle alpha in the given triangle.
4 Methods to Calculate the Tangent of Angle Alpha
How to Find the Tangent of Angle Alpha in the Semicircle | Geometry | Math
Brain Teaser 10 | Can You Find The Angle α?
ANGLE ALPHA = ?? | GEOMETRY CHALLENGE
Finding the Measure of Angle Alpha in a Triangle | Learn by Watching
The time is 10:00. Calculate the angle α between hour hand and minute hand. MathPrimary 20 Quiz
How To Calculate The Missing Angle In a Triangle
Unlocking Trigonometry: Understanding the Sum of Angle Formula
How to find an angle in analytical geometry grade 11 and grade 12. Angle of inclination
Find Missing Angle in a Right Triangle
Geometry Problem | Finding the Missing Angle | SAT Prep | Math Problem
Calculus 3 - Direction Cosines & Direction Angles of a Vector
Calculate the angle X and justify | Learn how to Solve the Geometry problem Quickly
Finding the Angle Between a Vector and an Axis in 3D
Calculate the angle X and justify | Learn how to Solve the Geometry problem Quickly
135 degree angle construction | 135° Angle
How To Calculate The Missing Side Length of a Triangle
How to Find the Moment from an Angle Force and Angled Lever Arm – Moment Problem 4
Determine the angle if the resultant is vertical | Vector Mechanics | Engineers Academy
Double Angle Identities & Formulas of Sin, Cos & Tan - Trigonometry
Комментарии
 0:05:20
0:05:20
 0:09:08
0:09:08
 0:09:44
0:09:44
 0:00:47
0:00:47
 0:08:58
0:08:58
 0:08:20
0:08:20
 0:00:51
0:00:51
 0:04:02
0:04:02
 0:03:02
0:03:02
 0:00:21
0:00:21
 0:14:33
0:14:33
 0:00:49
0:00:49
 0:15:03
0:15:03
 0:00:50
0:00:50
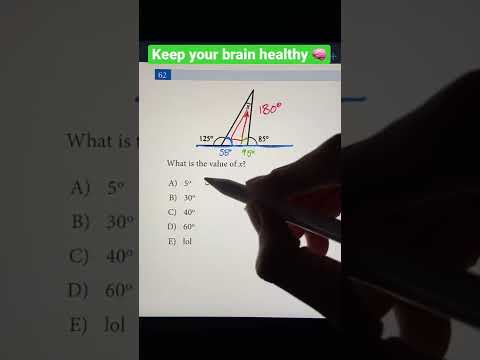 0:00:44
0:00:44
 0:12:50
0:12:50
 0:04:59
0:04:59
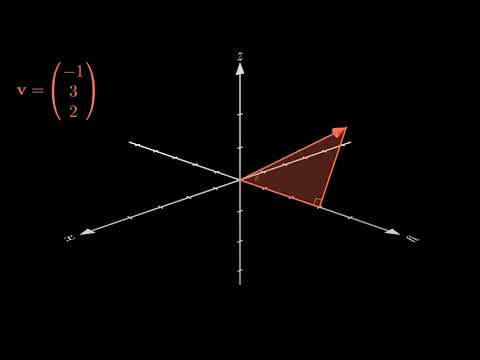 0:01:23
0:01:23
 0:03:18
0:03:18
 0:00:23
0:00:23
 0:29:56
0:29:56
 0:05:07
0:05:07
 0:10:50
0:10:50
 0:18:16
0:18:16