filmov
tv
Advanced Linear Algebra, Lecture 2.3: Algebra of linear mappings

Показать описание
Advanced Linear Algebra, Lecture 2.3: Algebra of linear mappings
This is somewhat of a "catch all" lecture where a number of important definitions about linear maps and basic results are given. It could have been given right after Lecture 1.1, where we originally defined linear maps, but it seems more appropriate to put in the section devoted to linear maps. The set of linear maps from X to U, denoted Hom(X,U), forms a vector space. If X=U, then they additionally define an algebra -- a vector space where we are also allowed to multiply vectors. Such linear maps are called endomorphisms, and the invertible ones form a subalgebra called the general linear group. These define similarity transformations, and an equivalence relation on Hom(X,X). We sprinkle some examples of these concepts and others throughout the lecture.
This is somewhat of a "catch all" lecture where a number of important definitions about linear maps and basic results are given. It could have been given right after Lecture 1.1, where we originally defined linear maps, but it seems more appropriate to put in the section devoted to linear maps. The set of linear maps from X to U, denoted Hom(X,U), forms a vector space. If X=U, then they additionally define an algebra -- a vector space where we are also allowed to multiply vectors. Such linear maps are called endomorphisms, and the invertible ones form a subalgebra called the general linear group. These define similarity transformations, and an equivalence relation on Hom(X,X). We sprinkle some examples of these concepts and others throughout the lecture.
Advanced Linear Algebra, Lecture 2.3: Algebra of linear mappings
Advanced Linear Algebra, Lecture 3.2: Symmetric and skew-symmetric multilinear forms
Advanced Linear Algebra 3: Bases
Advanced Linear Algebra 2: Spans & Linear Independence
Advanced Linear Algebra - Lecture 2: Subspaces
Grant Sanderson (3Blue1Brown): Best Way to Learn Math | AI Podcast Clips
Advanced Linear Algebra 4: Dimension of a Vector Space
Gilbert Strang: Linear Algebra vs Calculus
CSIR NET Dec. 2024 Test Series Launch | Test your Prep! | CSIR NET Exam by GP Sir
Advanced Linear Algebra 1: Vector Spaces & Subspaces
Advanced Linear Algebra - Lecture 3: Linear Combinations and Spans
Linear Algebra 1 (G30 Program) - Lecture 2: Matrices & Vectors
Advanced Linear Algebra, Lecture 7.2: Nonstandard inner products and Gram matrices
The Big Picture of Linear Algebra
Advanced Linear Algebra, Lecture 4.6: Generalized eigenspaces
Linear Algebra and it's Applications by Gilbert Strang #shorts
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
The Hardest Math Test
Legendary Book for Learning Abstract Algebra
Abstract Algebra Book with TONS of Content
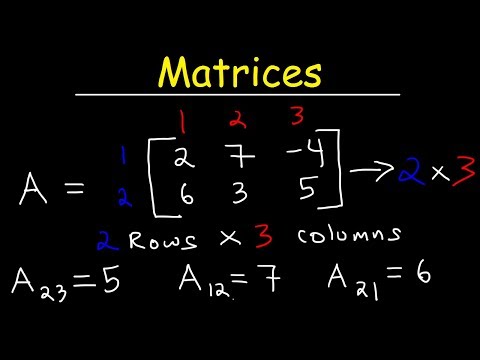
Intro to Matrices
Advanced Linear Algebra, Lecture 5.7: The norm of a linear map
Dear linear algebra students, This is what matrices (and matrix manipulation) really look like
A Book of Abstract Algebra
Комментарии
 0:35:24
0:35:24
 0:30:52
0:30:52
 0:47:30
0:47:30
 0:46:02
0:46:02
 0:16:20
0:16:20
 0:03:22
0:03:22
 0:48:32
0:48:32
 0:02:14
0:02:14
 0:01:58
0:01:58
 0:41:25
0:41:25
 0:19:37
0:19:37
 0:53:01
0:53:01
 0:40:49
0:40:49
 0:15:57
0:15:57
 0:26:41
0:26:41
 0:00:30
0:00:30
 0:13:52
0:13:52
 0:00:28
0:00:28
 0:01:00
0:01:00
 0:00:34
0:00:34
 0:11:23
0:11:23
 0:47:07
0:47:07
 0:16:26
0:16:26
 0:00:29
0:00:29