Riemann & Ricci Tensors & The Curvature Scalar

This video (GR - 17) starts with a fairly lengthy introduction to explain ‘where we are going’ - namely the journey from discussing the ‘Riemann Tensor’ to the ‘Ricci Tensor’ and then to the ‘Curvature Scalar’.

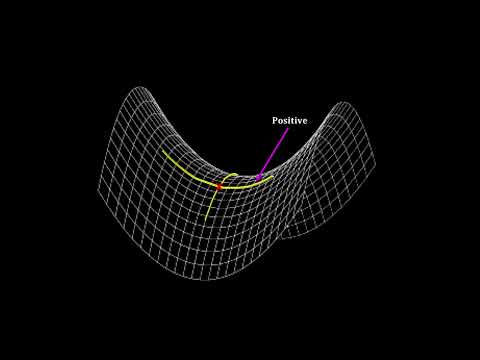
After almost 8 minutes of this introduction, we then begin by thinking about “Parallel Transport”, and the way in which vectors may change under such ‘transport’ if the space (or space-time) is curved. This idea leads on to a rather detailed explanation of the Riemann Curvature Tensor. However, the need for the Ricci Tensor is then suggested, and the discussion proceeds to show how that ‘comes out of’ the Riemann Tensor. Similarly, the third measure of curvature, the Curvature Scalar (‘Ricci Scalar’) is shown to be derived from the Ricci Tensor.

This video is part of a series of videos on General Relativity (GR-01 to GR-20), which has been created to help someone who knows a little bit about “Newtonian Gravity” and “Special Relativity” to appreciate both the need for “General Relativity”, and for the way in which the ‘modelling’ of General Relativity helps to satisfy that need – in the physics sense.

The production of these videos has been very much a ‘one man band’ from start to finish (‘blank paper’ to ‘final videos’), and so there are bound to be a number of errors which have slipped through. It has not been possible, for example, to have them “proof-watched” by a second person. In that sense, I would be glad of any comments for corrections ……. though it may be some time before I get around to making any changes.

By ‘corrections and changes’ I clearly do not mean changes of approach. The approach is fixed – though some mistakes in formulae may have been missed in my reviewing of the final videos, or indeed some ‘approximate explanations’ may have been made which were not given sufficient ‘qualification’. Such changes (in formulae, equations and ‘qualifying statements’) could be made at some later date if they were felt to be necessary.

This video (and channel) is NOT monetised

[michaelsatkevich]

You answered the question I had about needing a 4-d loop. I had asked @eigenchris the same thing 2 years ago! I'm pleased that I was not alone in my initial confusion. Thanks for a great video.

[warrenchu]

Illustrating the derivation by actual example showing the nitty gritty details really helped me understand tensor manipulation!
👍

[rk]

Thank you for this wonderful introduction to this subject!

[shintsuolson]

Great Video. Just wondering if you are familiar with volume form/element and how it is used to prove the Ricci tensor's role in volume changes along geodesics? I've been struggling to get my head around the proof.

[thorntontarr]

I struggle with Contraction used to simplify an expression. Yes, I understand what is happening - mathematically. However, is the information 'discarded' able to be physically 'discarded' without a loss of generality/physical meaning? In contracting the Riemann Curvature Tensor to the Ricci Curvature Tensor, you did go on to explain what the Ricci Curvature Tensor can be used to show the change in position of a cloud of dust as it moves on its geodesic path. OK, but what information would the full Riemann Curvature Tensor additionally provide - which is now gone and why is this contracted information appropriate for the Einstein Field Equations. Maybe all that will be revealed but it is not satisfying - to me - to contract without stating that it is a proper maths process.

One more like to you, Eddie. Your complete identification of the origin of the Riemann Curvature Tensor and the HUGE number of terms of each component of it (10 Christoffel Symbols which yield even more due to derivatives leading toward the Metric Tensor inclusion) is HUGELY satisfying to me. You have opened the door to such clarity in this whole process - many thanks.

FYI, I did find one index error in the graphic shown @49:45, the last row of last column of T(up lambda down mu, nu) should be T(up 3 down 3, 3) but is shown as T(up 0, down 3, 3). I only state this finding to highlight your superb attention to detail in entire graphic production not this single error; I can only speculate how many hours in this "one man band" approach you have had to expend on our behalf. I am in awe of your energy expended on our behalf.

[thevegg]

Hi Eddie, quick question. As we know a vector has both contra variant and covariant components. When people talk about contravariant they often refer to vectors like velocity. But when they talk about covariant, they talk about gradient. my question is why can’t they talk about velocity as well since velocity is a vector and it would have both contra variant and covariant components. on the flipside why can’t gradient have both contra and covariant relationship relationship?