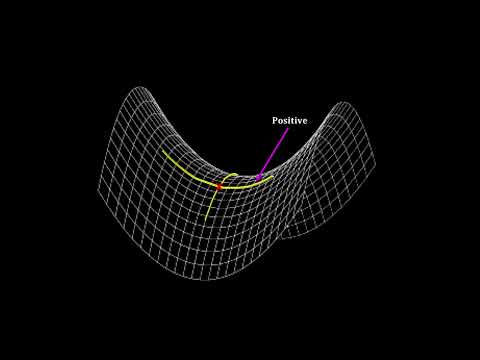
Tensor Calculus 24: Ricci Tensor Geometric Meaning (Sectional Curvature)

Previous videos on Riemann Curvature Tensor:

[jaeimp]

Nothing, absolutely nothing, makes GR more accessible than your presentations! Thank you for yet another superb effort at making some tough concepts intuitive. These video series is a gift to all curious people out there on par in quality and relevance with the work of Kahn Academy, 3Blue1Brown, Numberphile or Mathloger, and with the important difference that they cover a topic otherwise opaque without solid physics background.

[aliesmaeil]

thanks alot, I am a PHD math student, you are helping me alot with your videos.

[swamihuman]

- As all commenters have noted (praised), your presentation is superb.
- Thx for all you hard effort in creating this clear/concise/understandable content.
- I took 'Modern Physics' as part of my engineering degree, so got an introduction to GR, but of course did not go deep into the mathematics. Subsequently, I went on a broad/deep self-study into math (even became a math teacher). So, I have informally studied the Einstein Field Equations (EFE), along w/ tensors, and related matters. As a result, I was able to follow this video.
- One important takeaway for me from this vid is the explanation of how gravitation can be described as the consequence of geometry of curved space-time. Thx.

[Cosmalano]

My understanding of the non-vacuum EFE are so close now I can nearly taste them thanks to you. Watching you while I supplemented myself with other resources was the most enjoyable way to learn tensor calculus I think I could’ve had, you boosted my confidence immensely as a mathematician, and you opened up so many doors for me in theoretical physics. Thank you so much for this series.

[lucasmartinsbarretoalves]

this series is remarkably good. thank you so much for publishing it!

[izanagi]

While watching I had one question, why is it that at 24:37 the v vectors are expanded into linear combinations of the basis vectors? Weren’t they selected specifically as the e_n basis vector, meaning that the vector components v^j = 0 for all j ≠ n and with v^n = 1? In this case then, wouldn’t the curvature K(e_i, v) be 0 except for when j = k = n, in which case you’d continue to sum over i for the Ricci curvature, which would still make sense, but wouldn’t it mean that only one value from the Ricci tensor would impact the Ricci curvature, the R_(nn) entry, with the curvature itself equaling the value of that entry? I assume I made some error, but was just confused by this

[ericbischoff]

I did not expect Mary Poppins, but great analogy! Thanks.

[pythagorasaurusrex]

Cudos! This is the best series about Tensor stuff I have ever seen. You present your videos very visual, clear and focused. Just binge watching your mini series. I wished I had professors at my former university teaching this stuff like you do. You have a subscriber! Best wishes to you for 2021.

[morganhopkins]

Amazing content as usual! Keep up the fantastic work.

Also RIP to the Ricci scalar term in Einstein's equations at 2:17 😅

[ssrbaqri]

Having watched it just for initial few minutes, I get the intuition that I was so desperate to find but failed despite watching many videos... the moment u say that Ricci tensor gives the change of volume along a geodesic, I get that Eureka feeling.

[aramrashid]

You are the best! I have never seen someone better than you could talk about "Tensor". Your are amazing! and I recommend you to go on and be continue... We all are here so thankful that you do for us these fantastic lectures. We have learnt so so much from your videos. I wish one day after Tensor Calculus you could do some lectures also on Differential Geometry! I'm pretty much sure just you could exactly describe and illustrate how the stuffs works in differential geometry! I wish you the best! We love you man :)

[Wooferino]

Thank you. You're the best I've seen at navigating the details.

[ceoofracism]

and you early mentioned that those are basis vector, nl now you started to do linear combination at 24:40 can you tell what am i missing here?

[redrum]

This video is exactly what I've been looking for. Thank you so much

[domenicobianchi]

amazing content! relatively to the lat part, where after u found Ric(v, v)>0 you said the geodesic always converge, i have a doubt about what it means. Because if you walk from the equator to the poles they do converge, but if go from poles to equator they diverge. What is the right way to interpret this? thanks

[aidanmcsharry]

Hi eigenchris, hope all is well and thanks a load for these videos. This is probably a bit of a silly question, but I would like to just clarify it: at 24:34, you write out the vector v as a linear combination of the orthonormal basis, despite having said that ej dot v is zero, implying that v is parallel to a basis vector ek where k doesn't equal j (which is what you said a couple slides back). However, how, then, can you write out v as a linear combination of all of the other basis vectors, when it does not depend on them?

[theogoix]

This series is amazing, thanks eigenchris for making GR so accessible!
By the way, at 24:45 I don't understand why the vector v can be expanded as a linear combination of basis vectors, because, if I understood correctly, the basis itself is chosen such that it's orthonormal and v is a basis vector, so it should't have any component except itself. Do I miss something?

[erikstephens]

24:35- 24:40: Why expand v into (v^k)ek when we know v is one of the basis vectors?

[hannahlongsdale]

Hi Chris, when calculating the Ricci curvature how can you assume that the manifold will allow an orthonormal basis if it's not flat. Are you assuming just local flat co-ordinates rather than a global orthonormal coordinate system?

[waynechau]

I am really having trouble following the derivation of the Ricci Tensor Components at 25:26. When I look at other resources, they usually involve contracting the Riemann Tensor components in one of the lower indices. Can you please kindly clarify your method of derivation?

I worked on it for a bit by trying to assume v is a general vector and not part of the orthonormal basis (v = e_n). This approach the denominator becomes, ||v||^2- ||e_i||^2 ||v||^2 cos (theta)^2 = ||v||^2 sin(theta)^2 = ||v|| ||v|| sin (theta)^2 = (v x v) sin (theta) = 0 because of the cross product of v with itself. This means that for Ric(v, v) to be defined, v must be an orthonormal basis vector. In this case, I obtained Ric(v, v) = R_nn. What happened to the other elements not on the diagonal?