filmov
tv
Tangent on the Unit Circle
Показать описание
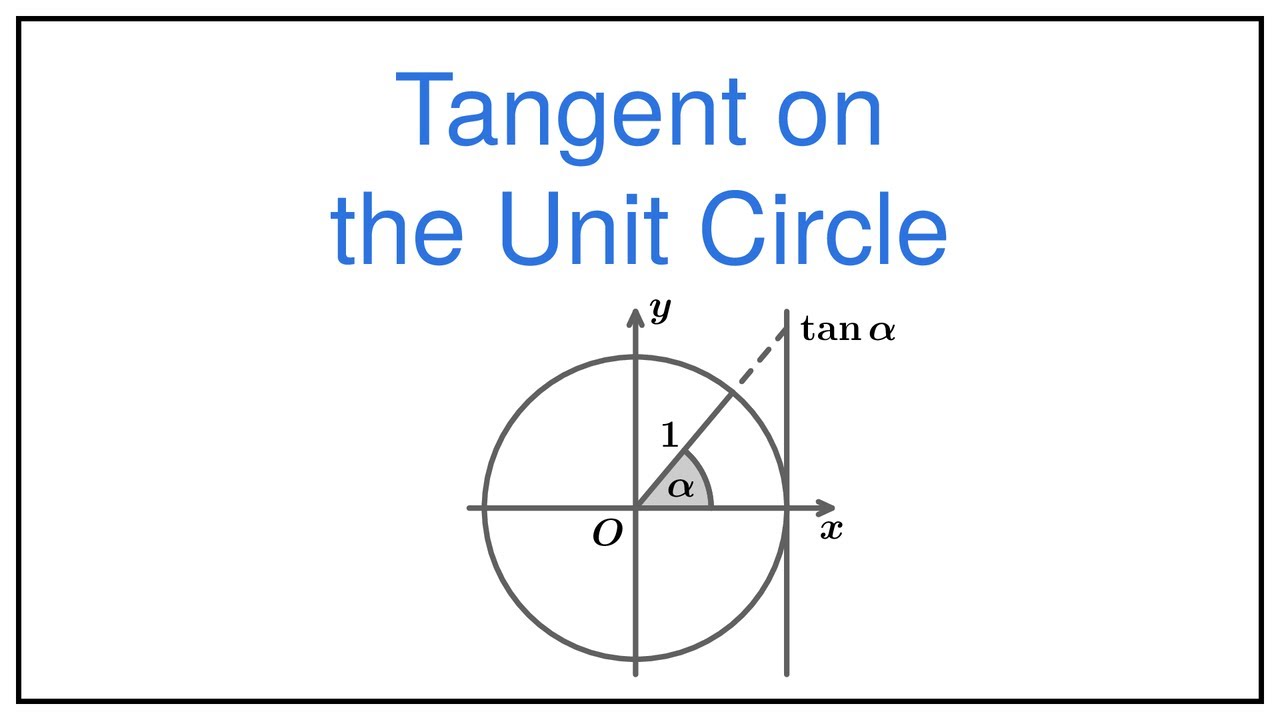
We start by recalling how can the tangent and the cotangent of an acute angle be expressed using the sine and the cosine. We then use those expressions as definitions of the tangent and cotangent of any angle. We also show how to visually represent the tangent of an angle on the unit circle.
Image credit (Thumbs Up):
0:07:18
Tangent on the Unit Circle
0:04:15
Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
0:00:31
Find TANGENT on the Unit Circle
0:02:33
Tutorial for evaluating tangent of an angle on the unit circle first quadrant
0:01:39
Visualizing Trigonometry: Tangent Function
0:06:18
Using the unit circle to find tangent
0:03:57
Tangent Function from Unit Circle
0:04:01
How do you evaluate for tangent function on unit circle
0:20:44
Simple Curve | Deflection Angle with English Units
0:05:20
A Geometric Understanding of the Trigonometric Functions (and proof of tan𝜃 ≡ sin𝜃/cos𝜃)
0:01:00
🤯 This ONE CIRCLE will make you finally understand trigonometry #shorts
0:00:27
Sine Curve and the Unit Circle
0:00:44
The Unit Circle Approach to Trigonometry #shorts
0:07:48
Tangent In The Unit Circle
0:10:06
Stop memorizing the unit circle
0:08:19
All 6 Trig Functions on the Unit Circle
0:30:34
08 - Calculate Sin, Cos & Tan w/ Unit Circle in Radians - Part 1
0:12:44
How To Remember The Unit Circle Fast!
0:05:03
Algebra 2 11.04c - The Tangent Ratio on the Unit Circle
0:07:19
Evaluate a point of the unit circle for sine, cosine and tangent
0:05:35
Tangent of the Common Angles on the Unit Circle
0:01:17
Learn to evaluate the half angle for tangent on the unit circle
0:11:32
18. Where is tangent on unit circle? Simple tangent equations.
0:00:56
What actually are sine and tangent?? A simple, circle-y explanation.
Комментарии