6. Partial Fraction Decomposition

O Horrible! O Disgusting! (But sometimes useful.) Get the skinny on partial fraction decomposition - everyone's least favorite integration technique - so that you can integrate rational functions when you must.

This is the sixth in what will eventually be a sequence of supplementary videos for a calculus class that I teach based on Chapters 4, 5, and 6 of my book 𝐹𝑢𝑙𝑙 𝐹𝑟𝑜𝑛𝑡𝑎𝑙 𝐶𝑎𝑙𝑐𝑢𝑙𝑢𝑠.

𝐹𝑢𝑙𝑙 𝐹𝑟𝑜𝑛𝑡𝑎𝑙 𝐶𝑎𝑙𝑐𝑢𝑙𝑢𝑠,
𝑇ℎ𝑒 𝐷𝑎𝑟𝑘 𝐴𝑟𝑡 𝑜𝑓 𝐿𝑖𝑛𝑒𝑎𝑟 𝐴𝑙𝑔𝑒𝑏𝑟𝑎,
𝑃𝑟𝑒𝑐𝑎𝑙𝑐𝑢𝑙𝑢𝑠 𝑀𝑎𝑑𝑒 𝐷𝑖𝑓𝑓𝑖𝑐𝑢𝑙𝑡,
𝐿𝑜𝑏𝑎𝑐ℎ𝑒𝑣𝑠𝑘𝑖 𝐼𝑙𝑙𝑢𝑚𝑖𝑛𝑎𝑡𝑒𝑑.

The first three are available for sale as paperbacks at Amazon, and as pdfs at Lulu. (The Lobachevski book is available at Amazon and the American Mathematical Society)

0:00 Intro (to bottom-heavy rational functions)
4:05 Rational = Polynomial + BH-rational
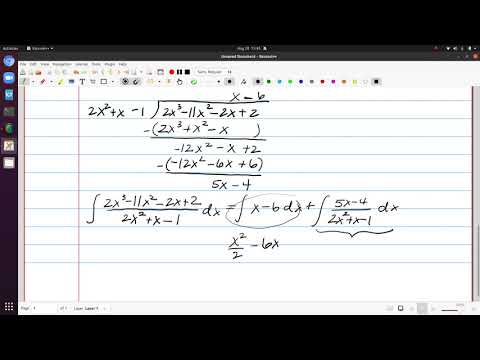
5:20 polynomial division
9:34 the FULL integral of 1/x
16:06 ∫(constant)/(linear)dx
20:03 a little algebraic trick
21:55 Partial Fractions (Case 1: distinct linear factors)
32:25 Another example
39:42 repeated linear factors
45:15 irreducible quadratic factors

[gustavodelgadillo]

The best explanations I've seen in the wild, I totally recommend buying the books to follow along, great content, thank You professor. Respect.

[CliffSedge-nufv]

At 29:00 I expected to see you take that short cut one step further to the "cover up" method.
Once the denominator is factored, you can sub in appropriate values of x (x: a factor equals zero) and then evaluate the function by pretending that factor equals 1 - covering it up.

[CliffSedge-nufv]

33:14 You can still use substitution on part of it.
First factor out a 2.
Let u = x³ - 4x, so du = 3x² - 4.
Numerator becomes 2[(7x - 6)dx + du]
Now the partial fractions step is easier.
It doesn't save a lot of work, but it is still an option, and can feel better for those who prefer substitution over partial fractions.
Combine it with the cover up method, and it is overall not too bad.