filmov
tv
Uniform Continuity on Compact Sets and Cauchy Sequences

Показать описание
We prove that every continuous function on a compact set is uniformly continuous.
#mikedabkowski, #mikethemathematician, #profdabkowski, #realanalysis
#mikedabkowski, #mikethemathematician, #profdabkowski, #realanalysis
Uniform Continuity and Compactness
Real Analysis | Uniform continuity and compact sets.
Uniform Continuity on Compact Sets and Cauchy Sequences
Uniform Continuity over Compact Sets
Real Analysis I (lec. 3.3.F) Uniform Continuity : Open, Closed, Compact Sets
Real Analysis I (lec. 3.3.D) Uniform Continuity : Open, Closed, Compact Sets
A continuous Function on a Compact Set is Uniformly Continuous
Continuous functions on compact sets are uniformly continuous - Lec 23
Real Analysis I (lec. 3.3.L) Uniform Continuity : Open, Closed, Compact Sets
Real Analysis I (lec. 3.3.B) Uniform Continuity : Open, Closed, Compact Sets
Real Analysis I (lec. 3.3.I) Uniform Continuity : Open, Closed, Compact Sets
Real Analysis I (lec. 3.3.E) Uniform Continuity : Open, Closed, Compact Sets
Continuous Functions on Compact Sets are Uniformly Continuous
Calculus 101 - Continuous Function on a Compact Set is Uniformly Continuous
Continuous Function from Compact Set is Uniformly Continuous: Math Notes for the Curious
Real Analysis: Uniform Continuity on Compact sets
Real Analysis I (lec. 3.3.C) Uniform Continuity : Open, Closed, Compact Sets
Real Analysis I (lec. 3.3.M) Uniform Continuity : Open, Closed, Compact Sets
Real Analysis I (lec. 3.3.H) Uniform Continuity : Open, Closed, Compact Sets
A continous function defined on a compact set is uniformly continous | Uniform Continuity | Msc/Bsc
Real Analysis I (lec. 3.3.A) Uniform Continuity : Open, Closed, Compact Sets
Real Analysis I (lec. 3.3.J) Uniform Continuity : Open, Closed, Compact Sets
uniform continuity and compact sets heine
402.4Y6 Continuous on Compact is Uniformly Continuous - Proof
Комментарии
 0:10:01
0:10:01
 0:08:45
0:08:45
 0:05:41
0:05:41
 0:24:54
0:24:54
 0:08:45
0:08:45
 0:05:36
0:05:36
 0:14:15
0:14:15
 0:26:47
0:26:47
 0:13:54
0:13:54
 0:10:14
0:10:14
 0:06:46
0:06:46
 0:08:28
0:08:28
 0:18:18
0:18:18
 0:10:33
0:10:33
 0:00:51
0:00:51
 0:11:33
0:11:33
 0:12:22
0:12:22
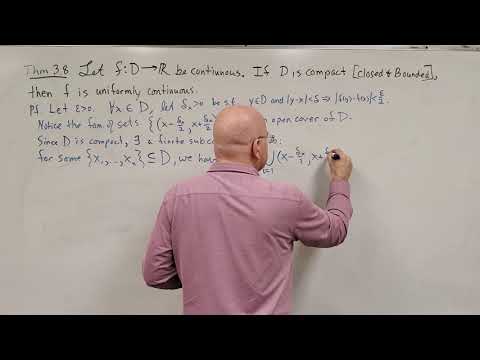 0:12:14
0:12:14
 0:12:24
0:12:24
 0:23:30
0:23:30
 0:06:36
0:06:36
 0:07:06
0:07:06
 0:15:57
0:15:57
 0:18:21
0:18:21