filmov
tv
Shells, Subshells, & Orbitals

Показать описание
What are Shells, Subshells, and Orbitals? | Chemistry
Shells, subshells, and orbitals | Atomic structure and properties | AP Chemistry | Khan Academy
Shells, Subshells, and Orbitals - BIOLOGY/CHEMISTRY EP5
Electron Configuration - Electron Subshells - Suborbitals - s, p, d, f - Orbitals - Chemistry
Orbitals, Atomic Energy Levels, & Sublevels Explained - Basic Introduction to Quantum Numbers
Elements, Atoms, Shells, Subshells And Orbitals
What ARE atomic orbitals?
A Better Way To Picture Atoms
Orbitals: Crash Course Chemistry #25
Atomic Orbitals
Shells, Sub-shells, and Orbitals l Understand the difference
Quantum Numbers, Atomic Orbitals, and Electron Configurations
Atomic orbitals 3D
Inside Atoms: Electron Shells and Valence Electron
Atomic Orbitals, Visualized Dynamically
Energy Levels, shells, SubLevels & Orbitals
Orbitals, the Basics: Atomic Orbital Tutorial — probability, shapes, energy |Crash Chemistry Academy...
Chemistry 101: Shells, Subshells, and Atomic Orbitals
Relationship of Quantum shells, Subshells, Orbitals & Electrons EXPLAINED [GCE A Level Chemistry...
How Small is an Atom?
6 Shells, Subshells, and Orbitals
Difference Between Orbits and Orbitals | Chemistry
Atomic Orbitals - p, d, f orbitals
How Many Orbitals are in the n=4 shell?
Комментарии
 0:06:00
0:06:00
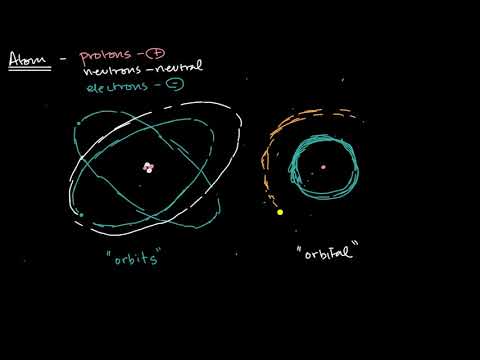 0:09:41
0:09:41
 0:09:23
0:09:23
 0:20:21
0:20:21
 0:11:19
0:11:19
 0:14:27
0:14:27
 0:21:34
0:21:34
 0:05:35
0:05:35
 0:10:52
0:10:52
 0:02:50
0:02:50
 0:13:04
0:13:04
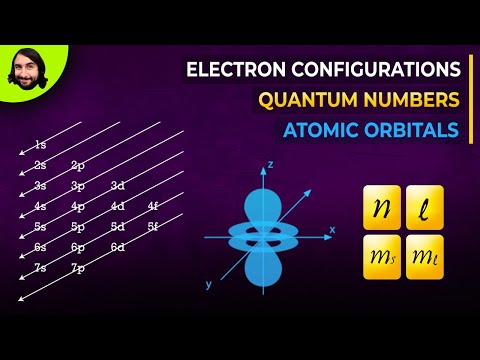 0:08:42
0:08:42
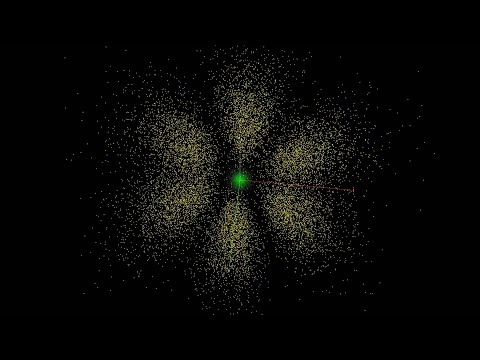 0:05:50
0:05:50
 0:03:25
0:03:25
 0:08:39
0:08:39
 0:03:24
0:03:24
 0:14:28
0:14:28
 0:04:36
0:04:36
 0:05:05
0:05:05
 0:04:52
0:04:52
 0:10:13
0:10:13
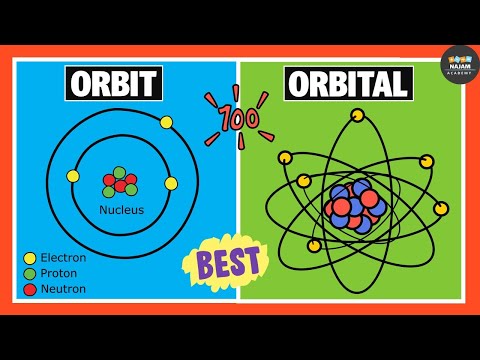 0:08:11
0:08:11
 0:06:05
0:06:05
 0:02:23
0:02:23