filmov
tv
Maximum Likelihood estimators of population mean and variance - part 1

Показать описание
In this video I explain how Maximum Likelihood Estimators of the population mean and variance can be derived, under the assumption of a normal error term in the population.
Maximum Likelihood estimators of population mean and variance - part 1
Maximum Likelihood estimation - an introduction part 1
Maximum Likelihood, clearly explained!!!
Maximum Likelihood Estimation ... MADE EASY!!!
Maximum Likelihood Explained
Maximum Likelihood estimators of population mean and variance - part 3
Methods of Estimation: Moments and Maximum Likelihood
Normal Distribution Maximum Likelihood Estimators and Estimates MLE
Maximum Likelihood Estimation (MLE) with Examples
Likelihood vs Probability Density Functions.Maximum Likelihood Estimates of Population Parameters.
Maximum Likelihood Estimation for the Normal Distribution
Maximum Likelihood Estimator (MLE) for theta in Uniform U[0, theta]
The Method of Moments ... Made Easy!
Maximum Likelihood Estimation for the Normal Distribution
1. Maximum Likelihood Estimation Basics
Maximum Likelihood estimators of population mean and variance - part 2
Least Squares as a Maximum Likelihood estimator
Finding MAXIMUM LIKELIHOOD ESTIMATOR for VARIANCE of NORMAL POPULATION || Is the Estimate Unbiased?
Maximum Likelihood Estimator of The Mean of The Normal Distribution
method of maximum likelihood function and it's properties
Maximum Likelihood Estimator | L20
Cross-validated Targeted Maximum Likelihood Estimation (CV-TMLE)
Maximum Likelihood estimation - an introduction part 2
Maximum Likelihood Estimation for Exponential Random Variables
Комментарии
 0:07:04
0:07:04
 0:08:25
0:08:25
 0:06:12
0:06:12
 0:09:12
0:09:12
 0:09:23
0:09:23
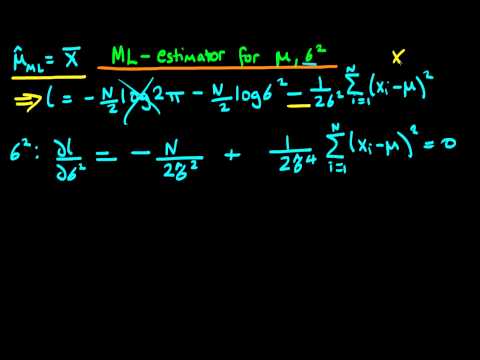 0:03:14
0:03:14
 0:20:17
0:20:17
 0:15:58
0:15:58
 0:15:50
0:15:50
 0:20:45
0:20:45
 0:07:12
0:07:12
 0:01:59
0:01:59
 0:09:02
0:09:02
 0:41:17
0:41:17
 0:06:33
0:06:33
 0:03:46
0:03:46
 0:07:38
0:07:38
 0:10:56
0:10:56
 0:10:08
0:10:08
 0:08:45
0:08:45
 0:34:17
0:34:17
 0:59:25
0:59:25
 0:07:08
0:07:08
 0:05:19
0:05:19