filmov
tv
Formula for a finite geometric series | Sequences, series and induction | Precalculus | Khan Academy

Показать описание
Missed the previous lesson?
Precalculus on Khan Academy: You may think that precalculus is simply the course you take before calculus. You would be right, of course, but that definition doesn't mean anything unless you have some knowledge of what calculus is. Let's keep it simple, shall we? Calculus is a conceptual framework which provides systematic techniques for solving problems. These problems are appropriately applicable to analytic geometry and algebra. Therefore....precalculus gives you the background for the mathematical concepts, problems, issues and techniques that appear in calculus, including trigonometry, functions, complex numbers, vectors, matrices, and others. There you have it ladies and gentlemen....an introduction to precalculus!
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Precalculus channel:
Комментарии
 0:09:38
0:09:38
 0:12:59
0:12:59
 0:05:45
0:05:45
 0:01:53
0:01:53
 0:00:59
0:00:59
 0:14:41
0:14:41
 0:02:42
0:02:42
 0:09:52
0:09:52
 0:53:57
0:53:57
 0:09:38
0:09:38
 0:07:14
0:07:14
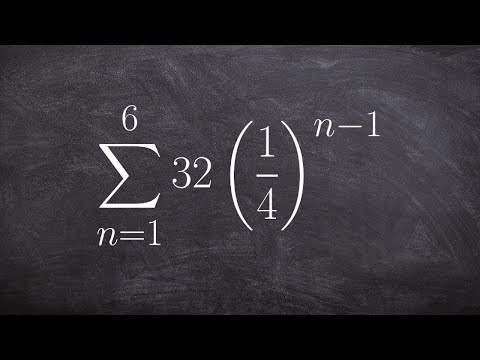 0:07:17
0:07:17
 0:06:59
0:06:59
 0:03:58
0:03:58
 0:01:09
0:01:09
 0:03:47
0:03:47
 0:10:48
0:10:48
![[Tagalog] Sum of](https://i.ytimg.com/vi/b0xArt7KXSY/hqdefault.jpg) 0:11:39
0:11:39
 0:19:50
0:19:50
 0:09:26
0:09:26
 0:03:48
0:03:48
 0:06:44
0:06:44
 0:08:15
0:08:15
 0:09:38
0:09:38