filmov
tv
Finite Geometric Sum Formula
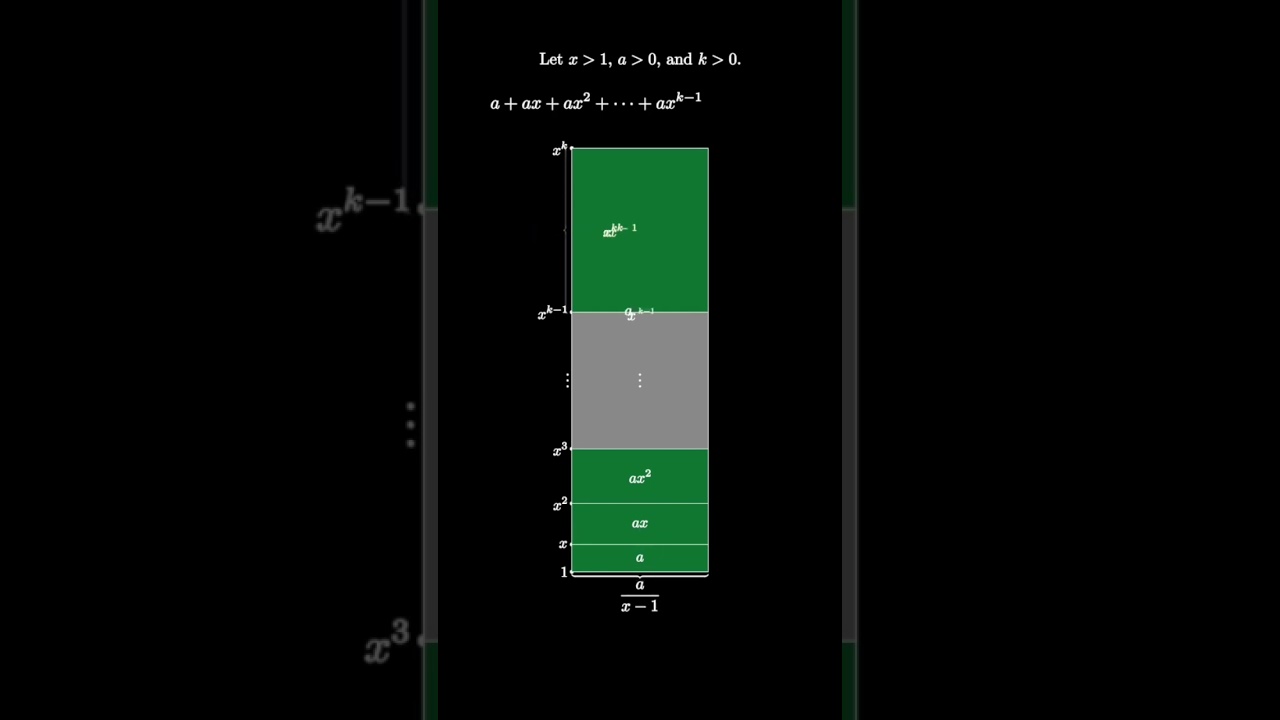
Показать описание
This is a short, animated visual proof demonstrating the finite geometric for any ratio x with x greater than 1. This series (and its infinite analog when x is less than 1) is important for many results in calculus, discrete mathematics, and combinatorics.
#mathshorts #mathvideo #math #calculus #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #geometricsums #series #finitesums #finiteseries #geometric
To learn more about animating with manim, check out:
#mathshorts #mathvideo #math #calculus #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #geometricsums #series #finitesums #finiteseries #geometric
To learn more about animating with manim, check out:
Finite Geometric Sum Formula
Finding The Sum of a Finite Geometric Series
How To Derive The Sum Formula of a Geometric Series
Formula for the Sum of a Finite Geometric Series
Learn how to determine the sum of a geometric finite series
The Geometry of Finite Geometric Sums (visual proof; series)
Geometric sum of powers of 7
formula for sum of finite geometric progression #shorts #youtubeshorts #maths
Formula for a finite geometric series | Sequences, series and induction | Precalculus | Khan Academy
How to Find the Sum of Finite Geometric Series
1-Minute Math: Sum of a Finite Geometric Series
Sum of a Finite Geometric Series
How to determine the sum of an finite geometric series
Geometric Sum (Finite) Formula
Infinite Geometric Series Sum
how to calculate the sum of a finite geometric series
➕Stop memorizing! Proving the formula for the sum of a finite geometric series. ➕
Finite Geometric Sums
A visual infinite sum like you’ve never seen!
Basic Finite Geometric Sum Ch8R1
How to find the finite sum of a geometric sequence
Geometric Sequences - The Sum of a Finite Geometric Sequence
Find the Sum of the Finite Geometric Sequence
How to determine the sum of a finite geometric sequence
Комментарии
 0:00:59
0:00:59
 0:12:59
0:12:59
 0:14:41
0:14:41
 0:18:54
0:18:54
 0:02:42
0:02:42
 0:01:53
0:01:53
 0:01:00
0:01:00
 0:00:16
0:00:16
 0:09:38
0:09:38
 0:03:48
0:03:48
 0:01:09
0:01:09
 0:05:32
0:05:32
 0:09:26
0:09:26
 0:08:16
0:08:16
 0:00:45
0:00:45
 0:08:17
0:08:17
 0:04:10
0:04:10
 0:11:26
0:11:26
 0:00:57
0:00:57
 0:00:56
0:00:56
 0:07:17
0:07:17
 0:08:36
0:08:36
 0:06:09
0:06:09
 0:03:47
0:03:47