filmov
tv
Pick's theorem: The wrong, amazing proof

Показать описание
A video on what proofs in mathematics are for, using Pick's theorem as an example.
Pick's theorem: The wrong, amazing proof
Pick's Theorem: to find the Area of Green Polygon instantly | Important Geometry skills explain...
Pick's Theorem (From Euler's Planar Graph Formula)
Formula for the Area of every Shape | Pick's Theorem
Pick’s Theorem⁉️ #math #mathstricks #lifehacks
Picks Theorem Calculator
Area of the Polygon of n sides| Pick's Theorem 🔥 of Geometry #logicxonomy #shorts
Pick's Theorem
Pick's theorem
Pick's Theorem Explained
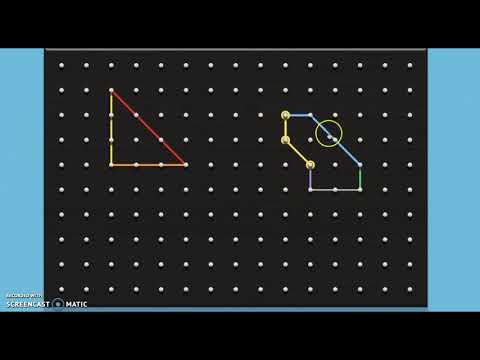
2(b). Pick's Theorem
Pick's Theorem 2.2
The Monty Hall Problem - Explained
Pick's Theorem 1.1
Math Contest Problem #18 - Pick's Theorem
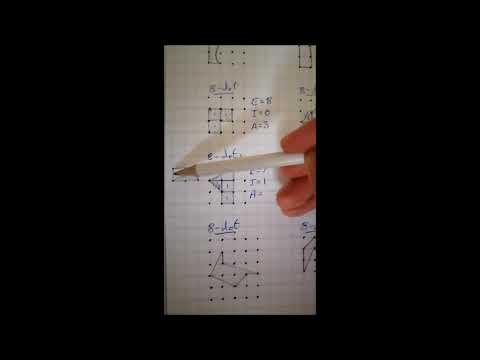
Proving The Pick’s Theorem
Instructional Series: Pick's Theorem
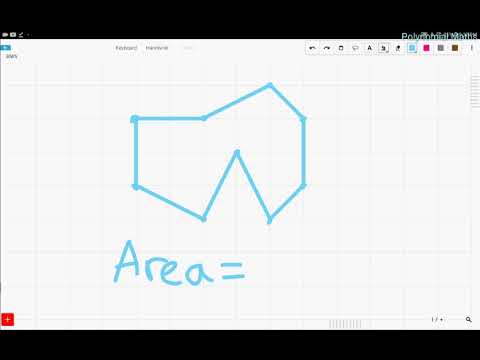
Finding the Area of Wierd Shapes Quickly..... How?! - Pick's Theorem
Ptolemy’s Theorem and the Almagest: we just found the best visual proof in 2000 years
Pick's Theorem Explained |Area of Regular and Irregular Polygons - Boundary Lattice Interior P...
Pick's Theorem - Harder Problems
For The Win Problem #2 (Pick's Theorem)
Pick's Theorem 8
Monty Hall Problem - Numberphile
Комментарии
 0:02:49
0:02:49
 0:09:09
0:09:09
 0:10:31
0:10:31
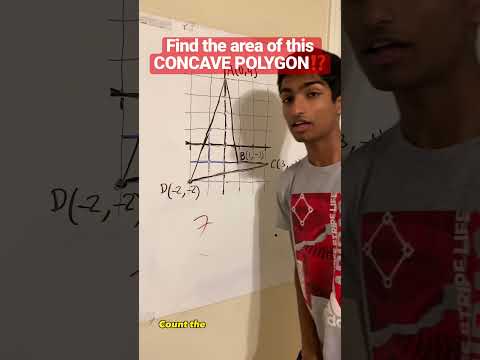 0:00:25
0:00:25
 0:01:38
0:01:38
 0:00:29
0:00:29
 0:04:10
0:04:10
 0:00:24
0:00:24
 0:02:12
0:02:12
 0:16:22
0:16:22
 0:02:03
0:02:03
 0:02:48
0:02:48
 0:02:08
0:02:08
 0:01:36
0:01:36
 0:09:08
0:09:08
 0:10:16
0:10:16
 0:02:26
0:02:26
 0:32:54
0:32:54
 0:10:40
0:10:40
 0:10:59
0:10:59
 0:04:19
0:04:19
 0:03:16
0:03:16
 0:05:30
0:05:30