Ptolemy’s Theorem and the Almagest: we just found the best visual proof in 2000 years

We are making history again by presenting a new visual proof of the 2000+ years old Ptolemy's theorem and Ptolemy's inequality.

00:00 Introduction
04:27 Geometry 101
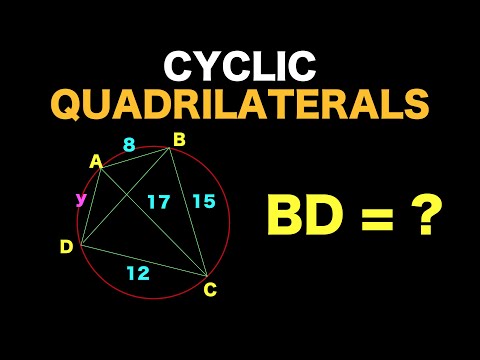
08:19 Applications
14:46 Ptolemy's inequality
18:34 LIES
25:35 Animated proofs
28:57 Thank you!
30:53 Degenerate Easter Egg

You can find a couple of full text versions of the Almagest here

For more background info check out the very comprehensive wiki pages on:
Ptolemy’s theorem
Ptolemy’s inequality
Claudius Ptolemy
The Almagest
Trigonometric identities
Cyclic quadrilateral
The optic equation

There are very interesting higher-dimensional versions of Ptolemy's theorem just like there are higher-dimensional versions of Pythagoras theorem. I did not get around to talking them today. Google ...

Highly recommended:

Here is a nice trick to make Ptolemy counterparts of Pythagorean triples. Take any two sets of Pythagorean triples:
5² = 3² + 4², 13² = 12² + 5², and combine them like this:
65² = 13² × 5²= 13²(4² + 3²) = 52² + 39²= 5²(12² + 5²) = 60² + 25².
Now combining the two right angled triangles 52-39-65 and 25-60-65 along the common diagonal in any of four different ways gives a convex quadrilateral with all sides integers. Note that you automatically get 5 integer lengths and then Ptolemy's theorem guarantees that the remaining side is a fraction. Scaling up everything by the denominator of that fraction gives one of the special integer-everywhere quadrilaterals. See also Brahmagupta quadrilaterals.

T-shirt: cowsine :)
Music: Floating branch by Muted and I promise by Ian Post.

Enjoy,

burkard

[Claudius_Ptolemy]

Thanks for making a video about my theorem!

[benpaz]

A day with a new Mathologer video is a better day

[josephyoung]

Didn't learn about Ptolemy's theorem until my late 20's, well after having learned calculus and other pretty sophisticated algebraic properties up through grade school and all. Should have been the first thing I learned.

[jotch_]

im already a big fan of long-form content in general, but this channel has such a distinct and enjoyable format that it easily sits in the top of the list. instead of continually building to a large and complex problem/explanation, its like you meander through a selection of related small problems that can be appreciated on their own or as a collective. it makes them very nice to watch and rewatch

[JCOpUntukIndonesia]

I've now realized how easy it is to miss the edge cases when using visual proof.

It's a crucial lesson in mathematical proof. I'll keep in mind when I'm dealing with visual proof in the future.

Thank you for the beautiful insight professor. Yet another gem you've shared with us 🎉

[christymccullough]

they don't want us knowing these things, hahaha. Thank goodness you are here!!!! What a time to be alive!!!

[kajdronm.]

What could go wrong at 28:16 ?
The corner, where the three tetrahedrons meet, corresponds to a spherical triangle.
The side lengths of wich are the angle wich meet there. These side length have to conform the triangle inequality, otherwise the corner can't be form.

Lucky as we are, the angles are just the angles of the corner, where the lower case edges meet. So all is fine.

[jacemandt]

The 2nd of the basic geometry theorems (that the inscribed angle is half the measure of the subtended arc) can also be used to easily prove the 1st: two opposite angles of a cyclic quadrilateral subtend arcs that clearly add to the entire circle, and their measures would then add to half of a circle, or 180°.

[Anmol_Sinha]

This was an amazing video. Ptolemy theorem is one of my fav theorems now!

[nicolaslj]

Your videos never disappoint, great work. This proof reminded me of that for the Pythagorean theorem that we take 3 copies, scale and bring together.

[williamhutchins]

When he flipped that triangle for the difference rule 14:07 I almost jumped out of my seat, Great work as always !

[PC_Simo]

24:30 For a while, I struggled with figuring out, why the ”>”-sign can’t become a ”<”-sign, straight away, as the quadrilateral becomes flat. But, I’ve finally got it: The transition between 3D and 2D is continuous; and, as such, the difference (Aa+Bb)-Cc must either stay positive (corresponding to the ”Strictly greater, than” -case), or, on its way to negative (corresponding to ”Aa+Bb < Cc”), it must pass through 0 (Aa+Bb = Cc), as you indicated, in your video on the ”Turning the wobbly table” -theorem (in a slightly different context). But; because, in a continuous transition, there is only 1 instant, where the quadrilateral is flat (and, therefore, the ”strictly greater than” -inequality doesn’t necessarily hold), the difference is always either positive or 0; and therefore, for all quadrilaterals, Aa+Bb >/= Cc. Very satisfying, I must say. 😌

[blackholesun]

00:00 intro.
04:30 Geometry 101
08:20 Applications
(Very excited to watch the whole thing!)

By the way, what are the notes being played in the piano jingle at the start? Thanks in advance 😁

[NoLongerBreathedIn]

Note that a proof of an equality that only works in a special case that's still sufficiently generic (in other words, where there are just as many free variables in the special case as in a generic situation) can often be generalized by analytic continuation. Inequalities need more careful handling.

[ibbiradar]

After preparing for competitive math Olympiads i hated geometry, this video has shown me the true light of how beautiful it is.

[shmupshmuppewpew]

Thanks for this clear explanation. As a non-mathematician I could still follow along and appreciate the elegance of the math here.
Also, your little giggle at 5:52 sent me. I love your enthusiasm!

[harrybarrow]

When I learned about imaginary numbers and their exponentials, it became much easier to remember and derive the angle sum formulae.

[mfaynberg]

Mr. Burkard, first of all thank you so much for your Mathologer channel. It is wonderful. I enjoy each and every video and keep waiting for the next one :) I would like to share one thought I've got after watching the latest episode about the Ptolemy's theorem - suspecting it is quite trivial and seems different to me only - for which I apologize in advance. Here is what I thought: the Ptolemy's imparity can be generalized a little bit. Let say, we have a quadrilateral - any in fact. Add the diagonals, i.e. get all vertices mutually connected. We will have a number of line segments (original shape's sides and diagonals). Now split those in pairs such that the segments in each pair would not have common vertices. Then apply that naming convention you've been using in your video, where one pair would have A and a segment, the next - B and b, and C and c. Then it seems that the rule Aa+Bb>=Cc will hold despite which pair is a''s, b's or c's, that is c-pair should not necessarily be of the diagonals. And it is pretty obvious based on the proof you have presented. Then, the case of equality follows with all vertices located on a circle, and c-pair being the diagonals. Thank you so much for your time - and again sorry for being not enough educated to recognize a trivial result. Am already waiting for your next video! Best regards, Mike Faynberg

[KettaTabuAaron-ne]

Thanks a lot mathologer...
But I'm badly missing videos on number theory and algebra... You seem to have gone full board to geometry.
Still waiting for your promised video on Abel's proof of why there can't be formulae for some higher degree polynomials

[gaetanomontante]

Oh, how I miss the days when such elegant demonstrations would come sooth my brain like butter on hot toast...