filmov
tv
Very Tricky Geometry Problem From Japan

Показать описание
GET MY EBOOKS
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
A Classically Hard Geometry Problem
What Is The Area? HARD Geometry Problem
Very hard geometry problem
Evil Geometry Problem
Hard Geometry Problem - Contest In Switzerland
A very tricky geometry problem: wrapping a semicircle with a quadrilateral
Incredible trick to solve this geometry problem
How To Solve The Hardest Easy Geometry Problem
TRICK to fix bad beveling in Blender
A Tricky Geometry Problem Solved In 2 Ways!
Clever method to solve a tricky geometry problem!
Missing Angles Geometry Problem | Tricky Math Question | JusticeTheTutor #maths #math #shorts
Genius student solved this in 1 minute - insanely hard geometry problem
why I think geometry is HARD
Incredibly hard geometry problem from Russia
VERY HARD South Korean Geometry Problem (CSAT Exam)
Can You Find Angle X? | Geometry Challenge!
Solution Of The Hardest Easy Geometry Problem In Mathematics
HARD Geometry Problem: Can You Solve The Horse Grazing Puzzle?
HARD Geometry Problem With Clever Solution. The Integer Rectangle
Geometry everyone should learn
Challenging Math Olympiad Problem | Geometry Question | Mathematics | 2 Methods
a nice geometry problem in the complex plane.
The hardest 'easy' geometry problem.
Комментарии
 0:05:10
0:05:10
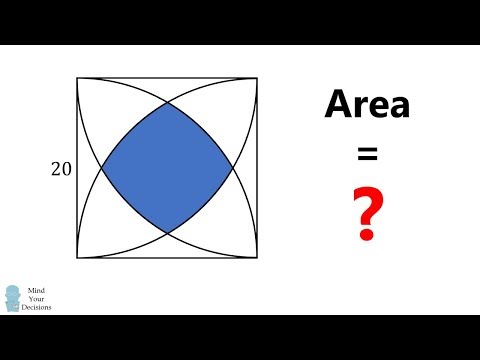 0:06:31
0:06:31
 0:07:22
0:07:22
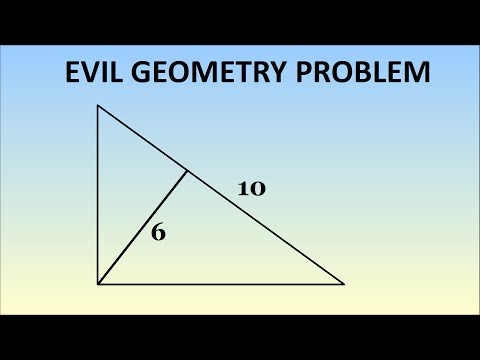 0:03:23
0:03:23
 0:04:32
0:04:32
 0:07:01
0:07:01
 0:05:39
0:05:39
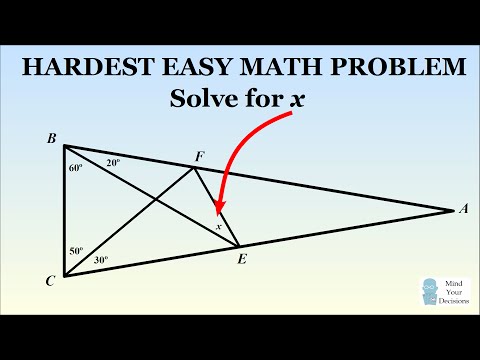 0:08:05
0:08:05
 0:00:16
0:00:16
 0:05:02
0:05:02
 0:03:15
0:03:15
 0:00:37
0:00:37
 0:09:24
0:09:24
 0:06:11
0:06:11
 0:09:27
0:09:27
 0:12:13
0:12:13
 0:08:44
0:08:44
 0:05:29
0:05:29
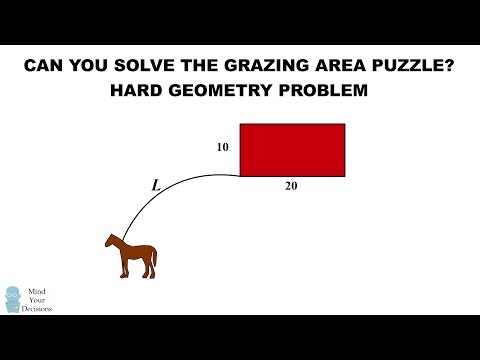 0:15:56
0:15:56
 0:06:20
0:06:20
 0:00:15
0:00:15
 0:25:44
0:25:44
 0:09:23
0:09:23
 0:16:40
0:16:40