filmov
tv
[Discrete Mathematics] Divisibility Examples

Показать описание
We do proofs with divisibility in this video.
LIKE AND SHARE THE VIDEO IF IT HELPED!
*--Playlists--*
*--Recommended Textbooks--*
Hello, welcome to TheTrevTutor. I'm here to help you learn your college courses in an easy, efficient manner. If you like what you see, feel free to subscribe and follow me for updates. If you have any questions, leave them below. I try to answer as many questions as possible. If something isn't quite clear or needs more explanation, I can easily make additional videos to satisfy your need for knowledge and understanding.
LIKE AND SHARE THE VIDEO IF IT HELPED!
*--Playlists--*
*--Recommended Textbooks--*
Hello, welcome to TheTrevTutor. I'm here to help you learn your college courses in an easy, efficient manner. If you like what you see, feel free to subscribe and follow me for updates. If you have any questions, leave them below. I try to answer as many questions as possible. If something isn't quite clear or needs more explanation, I can easily make additional videos to satisfy your need for knowledge and understanding.
[Discrete Mathematics] Divisibility Examples
DIVISIBILITY - DISCRETE MATHEMATICS
Number Theory | Divisibility Basics
Discrete Math - 4.1.1 Divisibility
Discrete Math 4.1.1 Divisibility
Induction Divisibility
Proving that divisibility is transitive
Number Theory Divisibility Proof
[Discrete Mathematics] Mathematical Induction Examples
Discrete Mathematics : - ( Divisibility test ) - 131. #discretemathematics #divisibilitytest
Disproving implications with Counterexamples
[Discrete Mathematics] Direct Proofs Examples
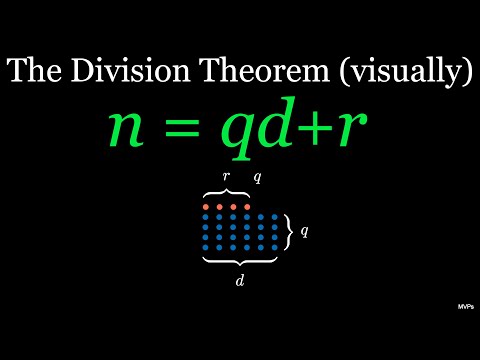
Division Theorem/Division Algorithm
Discrete Math - Number Theory and Divisibility
4.3 Direct Proof and Counterexample III: Divisibility
Direct Proofs Involving Divisibility
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
Mathematical Induction - Divisibility Tests (1) | ExamSolutions
Discrete Math - Divisibility
Properties of Divisibility | Number Theory | Mathematics
Divisibility (Discrete Math)
Discrete Math - 5.1.3 Proof Using Mathematical Induction - Divisibility
Discrete Math 4.1: Divisibility & Modular Arithmetic
Discrete Mathematical Structures, Lecture 3.4: Divisibility and primes
Комментарии
![[Discrete Mathematics] Divisibility](https://i.ytimg.com/vi/uBI6ZHyFq_Y/hqdefault.jpg) 0:04:43
0:04:43
 0:09:34
0:09:34
 0:07:13
0:07:13
 0:17:29
0:17:29
 0:15:42
0:15:42
 0:20:35
0:20:35
 0:11:09
0:11:09
 0:03:37
0:03:37
![[Discrete Mathematics] Mathematical](https://i.ytimg.com/vi/KW5k7ZsQmwo/hqdefault.jpg) 0:07:01
0:07:01
 0:24:22
0:24:22
 0:08:18
0:08:18
![[Discrete Mathematics] Direct](https://i.ytimg.com/vi/uDJfx4bK3Jc/hqdefault.jpg) 0:06:59
0:06:59
 0:02:33
0:02:33
 0:09:42
0:09:42
 0:08:32
0:08:32
 0:17:06
0:17:06
 0:05:45
0:05:45
 0:08:35
0:08:35
 0:08:20
0:08:20
 0:12:09
0:12:09
 0:22:03
0:22:03
 0:07:41
0:07:41
 0:34:55
0:34:55
 0:29:45
0:29:45