Find the Sum of Angles in the given Shape | How to Solve this Tricky Geometry problem Quickly

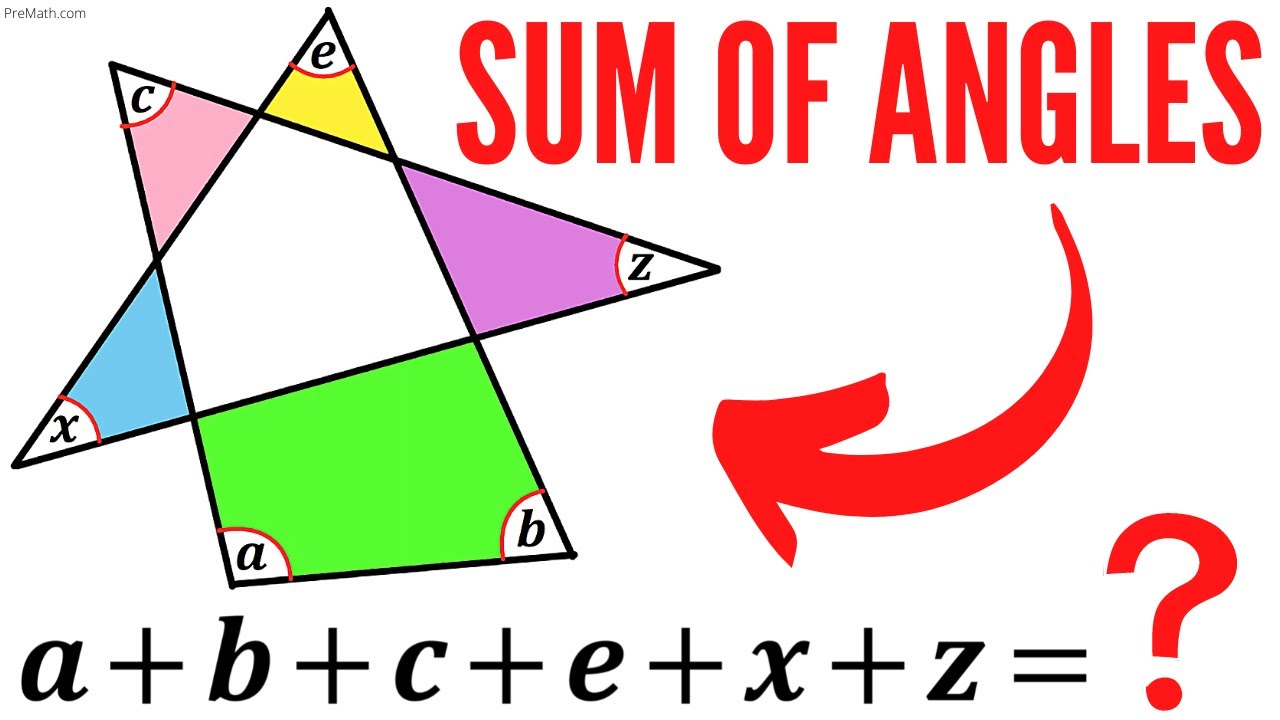
Learn how to find the sum of angles a+b+c+e+x+z in the given Shape. Solve this tricky geometry problem by using the Exterior Angle Theorem.

Need help with finding the sum of angles a+b+c+e+x+z in this complex Geometry question ? You're in the right place!

I have over 20 years of experience teaching Mathematics at American schools, colleges, and universities. Learn more about me at

Find the Sum of Angles in the given Shape | How to Solve this Tricky Geometry problem Quickly

#OlympiadMathematics #OlympiadPreparation #CollegeEntranceExam
#PythagoreanTheorem #Pythagorean
#HowtoCalculatethedistance #Findthedistanceofthelinesegment #LineSegment #length #distance #blackpenredpen #ComplementaryAngles #OlympiadMathematics
#FindtheAngle #HowtoSolvethisTrickyGeometryProblemQuickly #Triangle #Triangles
#ExteriorAngleTheorem #ExteriorAngle #FindtheSumofAngles

Olympiad Mathematics
pre math
Po Shen Loh
Learn how to find the angle X
How to Solve this Tricky Geometry problem Quickly
Find the Sum of Angles
Find the Sum of Angles in the given Shape
Exterior Angle Theorem
Exterior Angle
Exterior Angles
Learn how to find the sum of angles a+b+c+e+x+z

Subscribe Now as the ultimate shots of Math doses are on their way to fill your minds with the knowledge and wisdom once again.

[vidyadharjoshi]

Appears to be huge but simple. The answer is 360 deg. Focus on lower green rectangle.
Angle APN = 180 - Angle CPD, Angle CPD = 180 - ( Angle c + Angle z ) so Angle APN = Angle c + Angle z. Similarly
Angle PNB = Angle e + Angle x.

[scottwilson]

It's a "round twice" polygon, so the sum of the 6 external angles is 720 (2*360). One internal angle is 180-external; so the 6 internal angles are 6*180 - 6*external = 1080-720 = 360.

[devondevon]

not bad a problem
Using triangle CDP, angle P= 180- c+z, hence the angle inside the blue triangle to the left = c + z [180-(180-c-z]= c+z hence P outside of the green quadrilateral = c+z.
Using triangle EFN, angle N=180-e+x, hence the angle inside the purple triangle to the right = e+x, hence N outside of the green quadrilateral= e+x,
But a quadrilateral interior angles =360 hence a+b+c+e+x+z=360 answer

[covenslayer]

Your way is much easier. I kinda took a roundabout way. I circumscribed the figure with line segemts connecting b-d-e-c-f-a. Noticed that it was a 6 sided figure so sum of interior angles = 720. But I need to subtract out the 10 unneeded angles (angles adjacent to a, b, z, e, c, and x formed by the new figure). Then, I noticed that the inner figure was 5 sided, so the sum of the interior angles = 540, and those interior angles are vertical angels to one angle in each of the 5 triangles (formed from the new figure). So sum of all interior angles of a triangle = 180 and we have 5 so 180 * 5 = 900. And 900 - 540 = 360. This is the sum of all 10 angels that I need to subtract out of 720. So 720 - 360 = 360 Final Answer.

[BubuMarimba]

No theorems are required!
Consider triangles FEN & CPD:
x+e+N=180; x+e=180-N
c+z+P=180; c+z=180-P
Consider quadrilateral PABN: a+b+(180-P)+(180-N)=360
a+b+x+e+c+z=360

[TurquoizeGoldscraper]

I took the two triangles CDP and EFN, which are each 180 degrees. I labeled the other angles in those triangles as p and n, and I have c + x + p + e + x + n = 360 degrees. Then I looked at two pentagons, the white one, and the combined white and green one, and since pentagons always have 540 degrees, and they share 3 angles, then a + b = p + n. By substitution, I get a + b + c + d + x + z = 360 degrees.

[thomasaskew]

Wow. That was elegant and simple. It took me by surprise. Thanks.

[vacuumcarexpo]

The sum of the interior angles of Hexagon ABDECF minus the sum of the interior angles of five triangles plus the sum of the interior angles of the central pentagon is 720°－5×180°＋540°＝360°．

[math]

I was actually able to solve this tricky geometry problem. Thanks so much for the challenge bro.

[sandanadurair]

I considered two triangles
PCD &NFE
Sum of angles
C+z+p=180...1
X+e+N=180...2
Adding both
c+e+x+z+p+n=360....3
Quadrilateral
a+b+180-p+180-n = 360
Simplifying
p+n = a+b

Substituting this in 3
a+b+c+e+x+z =360

[audenwu]

Just draw the line CE, get angles e & f besides c & d, x+y is equal to e+f, so the sum of a+b+c+d+x+y is equal to a+b+c+d+e+f equal to the total of the quadrilateral 360 degrees.

[HassanLakiss]

Thank you for a nice geometry question and a nice and clear explanation.

[santiagoarosam]

The result can be easily visualized if we imagine an arrow superimposed on the “c-a” alignment; we move it until the point reaches the vertex “a” and we rotate the arrow on “a” inside the proposed figure until it overlaps with the alignment “a-b”; we move it until the end opposite the tip reaches the vertex “b” and on it we rotate it internally again until it is superimposed on the following alignment; the operation is repeated until the arrow ends up again superimposed on “a-c”. The arrow in its entire journey has only made a complete turn on itself, which means that the sum of the partial rotations is 360º.

[jakkima]

Connect B and D. Then NBD+NDB=e+x. We get a quadrilateral ABDC, the sum of the angles of which is 360 °

[HappyFamilyOnline]

Very nice explanation👍
Thanks for sharing😊😊

[epimaths]

Bài toán hình học tính góc. Hình học đẹp đó bạn. Cảm ơn.

[Teamstudy]

Ans :.a + b + c + d + e = 360 degree. Very Easy

[alster]

I knew it was 360° all along!

After pausing the last part and did further substitution, I already figured out the answer since the sum of the interior angles of a quadrilateral is 360°.

And same drill, fast forwarded to the end to double check at got it right

[mahalakshmiganapathy]

After your explanation it's easy to me,

[anatoliy]

Jeez! What a beautiful colorful curious task! And enough heavy for me. I dared to solve it in any other way but didn`t succeed. Thank you so much, sir! Each of your lessons is like a piece of living America! God bless you!