filmov
tv
A Non-Homogeneous Differential Equation
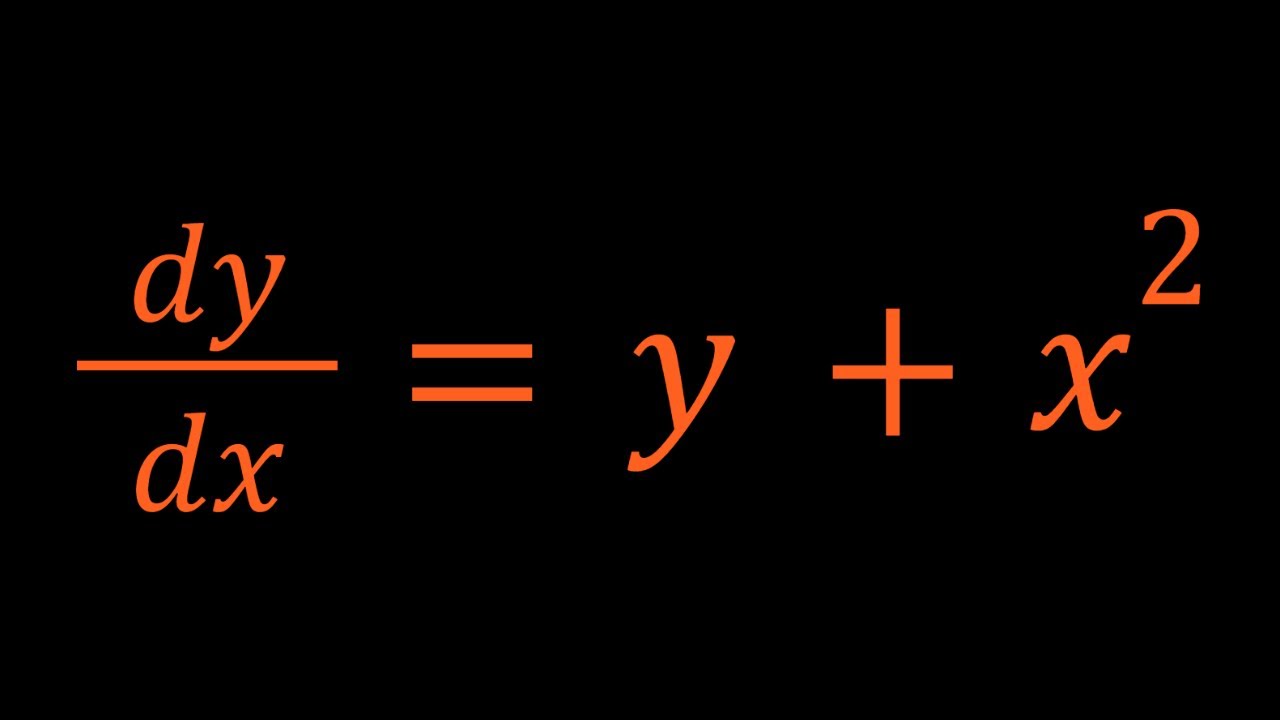
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #DifferentialEquations #Calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #DifferentialEquations #Calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Method of Undetermined Coefficients - Nonhomogeneous 2nd Order Differential Equations
Undetermined Coefficients: Solving non-homogeneous ODEs
A Non-Homogeneous Differential Equation
Nonhomogeneous 2nd-order differential equations
Second-Order Non-Homogeneous Differential (KristaKingMath)
Determine whether a differential equation is homogeneous
Nonhomogeneous First Order Linear ODE
Variation of Parameters || How to solve non-homogeneous ODEs
undetermined coefficients, diff eq, sect4.5#19
Method of Undetermined Coefficients - Non-Homogeneous Differential Equations
Non Homogeneous Linear Differential Equation With Higher Order | Problems | Examples | Maths
Solving Non-Homogenous Second Order Differential Equations
Variation of Parameters - Nonhomogeneous Second Order Differential Equations
Introduction To Second Order Linear NonHomogeneous Differential Equations
🔵21a - Method of Undetermined Coefficients 1 - G(x) = Constant: 2nd Order Non - Homogeneous D.E
Second order non homogeneous differential equation
How To solve Second Order Linear Non Homogeneous Differential Equations | Lesson 1
homogeneous and non-homogeneous differential equation | How to check homogeneous & non-homogeneo...
🔵21c - Method of Undetermined Coefficients 3 - G(x) = Exponential Functions - Non - Homogeneous D.E...
Differential Equations: Non-homogeneous Linear DE
2.5 Nonhomogeneous Equations and Undetermined Coefficients
A-Level Further Maths I5-01 2nd Order Differential Equations: Introducing Non-Homogeneous DEs
0205 Differential Equations Homogeneous and Non homogeneous Equations
Differential Equations: Undetermined Coefficients - Superposition Approach
Комментарии
 0:41:28
0:41:28
 0:12:44
0:12:44
 0:07:00
0:07:00
 0:26:58
0:26:58
 0:21:16
0:21:16
 0:01:47
0:01:47
 0:04:14
0:04:14
 0:10:56
0:10:56
 0:16:42
0:16:42
 0:25:25
0:25:25
 0:12:11
0:12:11
 0:25:18
0:25:18
 0:11:36
0:11:36
 0:11:21
0:11:21
 0:15:25
0:15:25
 0:12:21
0:12:21
 0:09:25
0:09:25
 0:05:18
0:05:18
 0:30:13
0:30:13
 0:06:17
0:06:17
 0:49:36
0:49:36
 0:02:24
0:02:24
 0:06:54
0:06:54
 0:22:14
0:22:14