Three-Body Problem: A Precise Simulation

The motion of three free bodies in gravitational interaction is one of the simplest examples of chaotic behaviour in nature. Such behaviour is characterised by complex non-periodic orbits, which usually exhibit a high sensitivity on small variations in the initial conditions – a feature known as the butterfly effect.

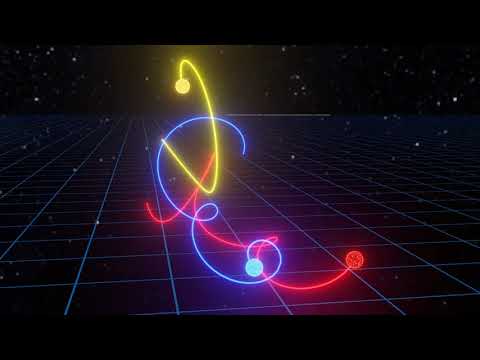
This video shows a high-precision simulation of the special three-body problem, where three identical point masses are initially at rest at the vertices of a Pythagorean triangle of axes ratios 3:4:5. As in almost all three-body problems, one of the bodies gets eventually kicked out of the system, while the other two remain stuck together forever.

The orbits of the three masses have been computed iteratively, using the "nbody" package of the R programming language. The solution shown here used a 4th order Yoshida integrator with an adaptive block time-step, chosen small enough to ensure that the solution is exact within less than a pixel for the whole duration of the simulation.

The masses M of the three bodies and the length unit L of the triangle are irrelevant in the sense that the orbits are geometrically similar for any positive choices of M and L – this is the scale invariance of gravitation. The overall scale of the orbits is proportional to L and the time taken to move through them is proportional to sqrt(L^3/(GM)), where G is the gravitational constant.

Credits:
Software: R-language with nbody package

Related literature:

[ririban]

red: Ive had enough of this toxic relationship bye

[squamousthomas]

So are we all reading the same book right now?

[cosmicblueshift]

Beautiful laws of physics. It's strangely addictive

[giandrago]

This has been one of the most interesting videos I've ever seen on YouTube. Thank you.

[gonegahgah]

Bodies won’t initially be at zero velocity to each other. I’d be very interested in some “natural” examples where 3 body problems came into being. Maybe one where two bodies are orbiting each other and an interloper enters the system?

[captainzeppos]

The only reason to be here is because of the best sci-fi trilogy of the last 50 years.

[pndiodh]

0:42 finally trisolarians get peace and start to develop dimension breaking skills

[denisgavrila]

Red: NO I DONT WANNA LEA- *leaves*
Blue And Yellow:
Lets PLAY OH NO DONT LEAV-

[zoecarlibur]

Is anyone here reading the book, Spoiler below ⚠












this really helps understand the movement of the suns the world of 3 body 👍

[themetadaemon]

Something that always bothered me about these simulations. There appear to be collisions. Are there?

[jhunz]

Have to watch this, as told to me by Sophons, before i go back to the game in a bizarre golden helmet to save a child!

[MarkoBotsaris]

The “unusual” motion per se is honestly beside the point, especially as for the initial conditions here the system rapidly decouples into two integrable, entirely predictable systems. The essence of the three-body problem is exponential divergence of trajectories from very small differences in initial conditions - the feature that essentially makes the general solution uncomputable. That lack of computability, even in principle, is the essential point both for its role in the history of mathematics, and for its meaning in the sci-fi books of the same name - both literally and as a metaphor in the story. Numerical simulations are pretty great at demonstrating this as you could have shown trajectories for very small changes in initial conditions plotted together and diverging. A big missed opportunity IMHO.

[lingarajpetla]

This looked like some kind of a love triangle 😅

[sslavi]

I guess the divergence of paths at the end of the video is just temporary (and hence apparent), because the initial potential enegy of the system cannot be sufficient for any of three bodies to reach the escape velocity. If the simulation had run long enough, the bodies would come back into the screen.

[AcrossThePacific.]

It would be so cool if someone made a screensaver out of random initial conditions of a three body system. I’d totally watch it and forget time.

[kingki]

Remind me to get hydrated after 100 years

[No-one]

Deep inside I feel empathy for the Alien invades earth

[Mrhus]

The Flower of Life is the solution to the three body problem. All K-Paxians know this.

[terryanisaurasrex]

The universes most common answer to three body problem is to make it a two body problem

[jjjyrtrrr]

did you include the relativistic terms to make it precise? or it is just Newton body motion