filmov
tv
A challenging rational equation
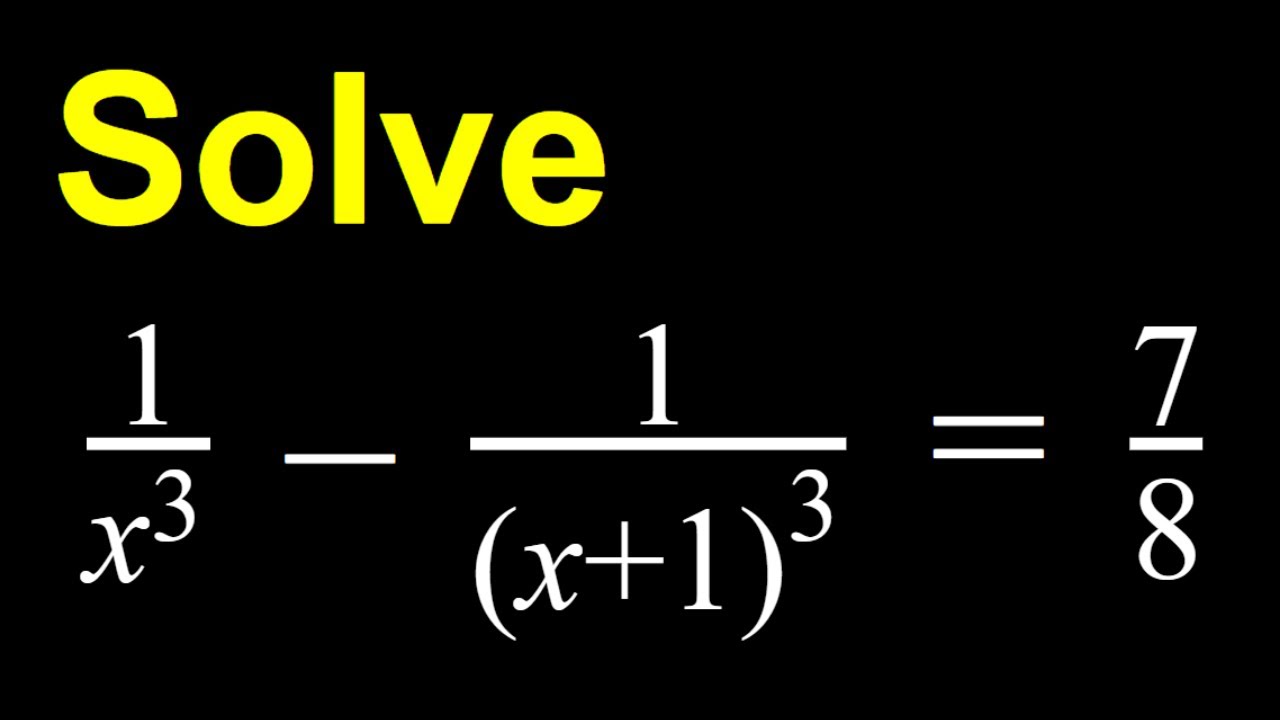
Показать описание
This video is about an rational equation with a very interesting solution
If you want to share a picture of your solution/ideas, send me a tweet at @SyberMath and comment here with the link to the tweet.
#ChallengingMathProblems #RationalEquations
EXPLORE:
If you want to share a picture of your solution/ideas, send me a tweet at @SyberMath and comment here with the link to the tweet.
#ChallengingMathProblems #RationalEquations
EXPLORE:
A challenging rational equation
Solving Rational Equations Easier Method
Solving Rational Equations
A Challenging Rational Equation | #algebra #polynomials
Rational Equation Challenge: Can You Solve the Given Rational Equation? #math #maths #equation
Rational Equation Challenge
Math tutorial for solving rational equations
Rational equations difficult
Challenging mathematics for all exams #education #sciencelab #tech #motivation #physicalscience
Equation Challenge: Solve a Rational Equation with a Complex Fraction
A Rational Equation
A Nice Rational Equation Challenge | Math Olympiad | Algebra
Solving a rational equation in an unusual way. An algebraic challenge...
Math Challenge | Grades 7-8 | Solving Rational Equation [with English subtitles]
Solving a rational equation with two solutions
Applying rational equations 1 | Polynomial and rational functions | Algebra II | Khan Academy
Fun Rational Equation
4.5 Sovling difficult rational equations #3
Challenging Rational Equation ! NO Guessing
Solving a basic rational equation by multiplying each term by the LCD
Solving a Rational Equation in Two Ways
A Rational Equation Inspired by @drpeyam
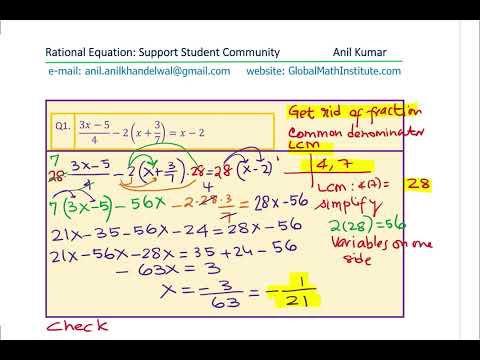
Challenge Rational Equations Prepare for GCSE SAT Math or Any Exam Join Anil Kumar Classes
Solve Rational Equation Challenge for Middle School Students Keep Sharing and Learning Anil Kumar
Комментарии
 0:13:14
0:13:14
 0:04:33
0:04:33
 0:11:03
0:11:03
 0:13:14
0:13:14
 0:00:55
0:00:55
 0:02:08
0:02:08
 0:06:32
0:06:32
 0:05:29
0:05:29
 0:01:01
0:01:01
 0:00:52
0:00:52
 0:08:20
0:08:20
 0:12:44
0:12:44
 0:10:55
0:10:55
 0:04:35
0:04:35
 0:08:50
0:08:50
 0:05:26
0:05:26
 0:01:32
0:01:32
 0:06:12
0:06:12
 0:08:07
0:08:07
 0:04:12
0:04:12
 0:11:03
0:11:03
 0:06:52
0:06:52
 0:08:08
0:08:08
 0:17:42
0:17:42