filmov
tv
Math 391 Lecture 3 - The integrating factor method and homogeneous 1st order ODEs
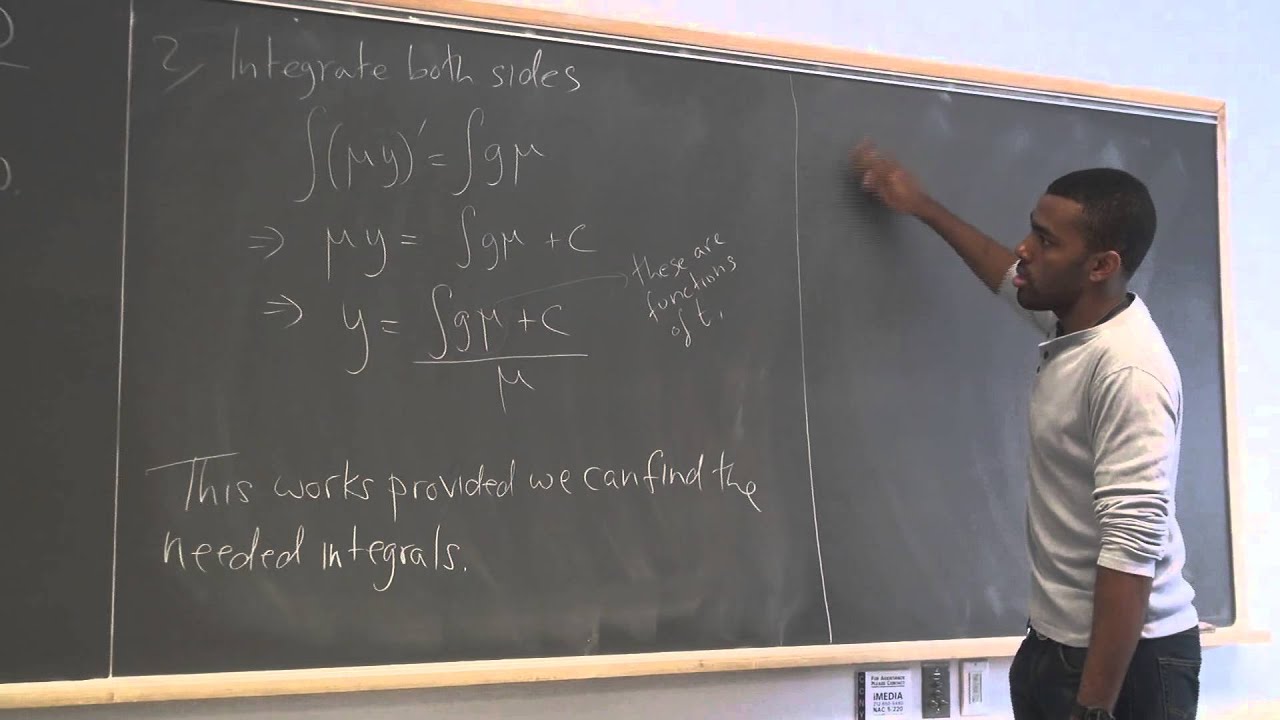
Показать описание
In this lecture, we continue to discuss ways of solving various first order ODEs, which is the focus of chapter 2 of Boyce/DiPrima. We focus our attention first on first order linear ODEs, in particular, those that are not separable. We look at the method of integrating factors to solve such equations, after deriving what the needed integrating factor must be. We then move on to homogeneous differential equations--a bit of a misnomer, since we will see later that "homogeneous" usually refers to something else--but we look at ways to turn such equations into separable ones with a powerful substitution technique. We did several examples of applying the integrating factor method here, but only one example of dealing with homogeneous 1st order ODEs; we will pick up with more examples next time.
Math 391 Lecture 3 - The integrating factor method and homogeneous 1st order ODEs
Math 391 1XC Lecture 3 - Homogeneous First Order Differential Equations
Math 391 Lecture 15 - Short review of chapter 3 - Test 2 preparation
Math 391 Lecture 2 - Intro to differential equations - definitions and separation of variables
Math 391 Lecture 4 - Homogeneous 1st order ODEs and modeling with first order linear ODEs
Math 391 1XC Lecture 5 - Continuous Compounding; Newton's Cooling Law; Exact Differential Equat...
Math 391 Lecture 18 - Series Solutions to second order linear differential equations contd
Math 391 1XC Lecture 4 - Modeling with First Order ODEs: Mixture Problems and Continuous Compounding
11 | MHT-CET | Physics | Motion in a Plane | Lecture 2 | MCQs | PYQs
Math 391 1XC Lecture 20 - Sturm-Liouville Theory; The Eigenvalue Problem; and The Heat Equation
Math 391 1XC Lecture 14 - EUT for first order nonlinear ODEs; Intervals of solutions; Series Review
Math 391 1XC Lecture 2 - Population Models and First Order Linear Differential Equations
Math 391 1XC Lecture 7 - Misc ODEs;The Bernoulli First Order ODE, Complex Numbers; Euler's Iden...
Math 391 Lecture 23 - Separation of Variables for PDEs and the Heat Equation
Math 205 Lecture 3 - Domains, Composition and Transformations of functions; Straight lines
Genius IQ Test-Maths Puzzles | Tricky Riddles | Maths Game | Paheliyan with Answers | Tricky Paheli
Math 391 Lecture 5 - Modeling with linear equations continued - Mixture Problems
Math 391 1XC Lecture 1 - Order and classification of a ODEs; Separable ODEs; Direction fields
Differential Equations, Lecture 3.3: The method of undetermined coefficients
Math 391 1XC Lecture 21 - Final Exam Review
delhi civil defence m aise ho rhe h kaam #shorts #delhi #indian
Math 391 1XC Lecture 13 - Why are there n solutions to an nth order LODE; More techniques for HOLDEs
Differential Equations: Lecture 2.2 Separable Equations
Math 391 Lecture 1 - Intro and a very brief (and incomplete) overview of ODEs
Комментарии
 1:00:56
1:00:56
 1:16:41
1:16:41
 0:39:17
0:39:17
 0:48:22
0:48:22
 0:58:20
0:58:20
 1:38:26
1:38:26
 1:04:18
1:04:18
 1:37:14
1:37:14
 0:38:51
0:38:51
 1:52:46
1:52:46
 1:44:07
1:44:07
 1:37:23
1:37:23
 1:39:22
1:39:22
 1:01:53
1:01:53
 1:31:04
1:31:04
 0:00:24
0:00:24
 0:52:39
0:52:39
 1:38:04
1:38:04
 0:54:39
0:54:39
 1:51:41
1:51:41
 0:00:13
0:00:13
 1:58:02
1:58:02
 0:56:16
0:56:16
 0:48:45
0:48:45