filmov
tv
Solving Polynomial Equations 1: A power series approach | Research Level Mathematics | Wild Egg Math

Показать описание
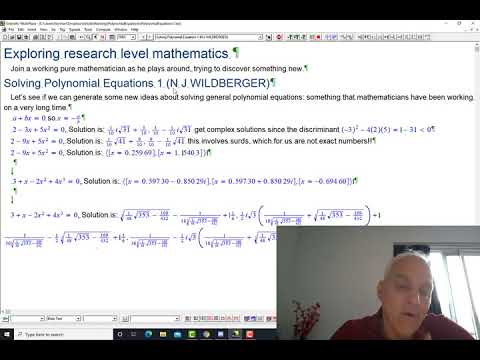
How do you solve a polynomial equation? Let's play around with this famous problem and see if we can tinker our way to some new insights. Along the way we strengthen our understanding of polynomial or polynumber arithmetic, and its extension to on-polynumbers or power series, and get some experience with the power of Scientific Workplace for writing and working on mathematics.
This is the first video in a series where we will reconfigure the landscape for the classical algebraic problem of solving a polynomial equation. Formulas involving so-called "radicals" --- which themselves cannot be exactly evaluated --- are finessed, and we move the subject in an entirely different direction, by harnessing the utility of formal power series and rational extensions of them.
The entire series will become available to Members of the Wild Egg Maths channel over the next few months -- be sure to click the JOIN button to participate in an exciting adventure to EXPLORE RESEARCH LEVEL MATHS. This is a unique opportunity to be guided into the fascinating world of mathematical research by one of the world's leading mathematical educators.
************************
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************************************
Here are the Insights into Mathematics Playlists:
****************
This is the first video in a series where we will reconfigure the landscape for the classical algebraic problem of solving a polynomial equation. Formulas involving so-called "radicals" --- which themselves cannot be exactly evaluated --- are finessed, and we move the subject in an entirely different direction, by harnessing the utility of formal power series and rational extensions of them.
The entire series will become available to Members of the Wild Egg Maths channel over the next few months -- be sure to click the JOIN button to participate in an exciting adventure to EXPLORE RESEARCH LEVEL MATHS. This is a unique opportunity to be guided into the fascinating world of mathematical research by one of the world's leading mathematical educators.
************************
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************************************
Here are the Insights into Mathematics Playlists:
****************
Комментарии
 0:27:31
0:27:31
 0:14:19
0:14:19
 0:09:20
0:09:20
 0:14:16
0:14:16
 0:04:15
0:04:15
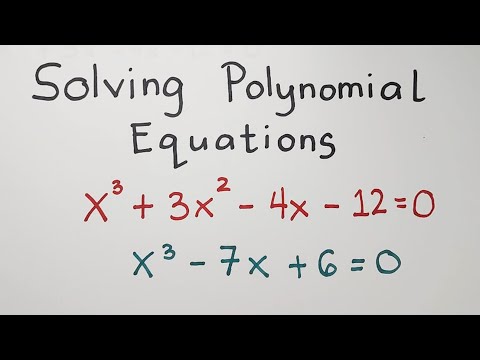 0:12:02
0:12:02
 0:10:44
0:10:44
 0:17:45
0:17:45
 0:01:01
0:01:01
 0:37:37
0:37:37
 0:12:29
0:12:29
 0:02:43
0:02:43
 0:15:43
0:15:43
 0:06:41
0:06:41
 0:30:31
0:30:31
 0:02:43
0:02:43
 0:10:00
0:10:00
 0:11:54
0:11:54
 0:08:22
0:08:22
 0:00:50
0:00:50
 0:03:50
0:03:50
 0:09:05
0:09:05
 0:17:57
0:17:57
 0:34:26
0:34:26