filmov
tv
Inverse Hyperbolic Trigonometry as Logarithms: sech^-1(x)
Показать описание
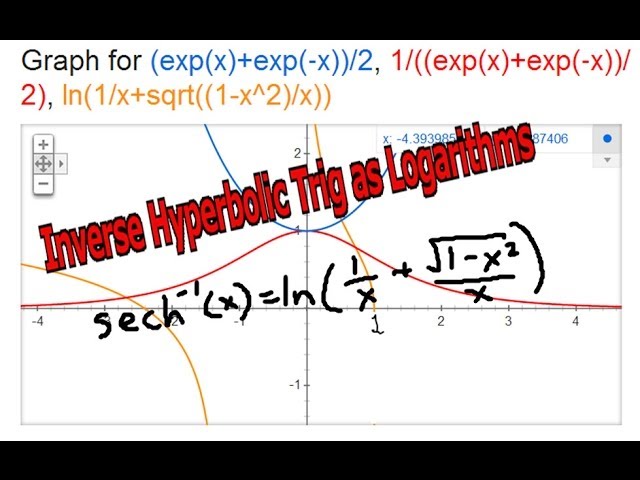
In this video I go over converting inverse hyperbolic trig functions to logarithms and prove that the function inverse hyperbolic secant or sech^-1(x) is equal to ln(1/x+sqrt(1-x^2)/x).
Related Videos:
------------------------------------------------------
Related Videos:
------------------------------------------------------
0:07:57
Inverse Hyperbolic Trigonometry as Logarithms: tanh^-1(x)
0:11:50
Inverse Hyperbolic Trigonometry as Logarithms: cosh^-1(x)
0:09:38
Inverse Hyperbolic Trigonometry as Logarithms: sinh^-1(x)
0:11:35
Inverse Hyperbolic Trigonometry as Logarithms: csch^-1(x)
0:08:14
Inverse Hyperbolic Trigonometry as Logarithms: coth^-1(x)
0:09:10
Evaluating Inverse Hyperbolic Functions
0:08:36
Inverse hyperbolic cosine [cosh^-1(x)] as a logarithm
0:13:42
Inverse Hyperbolic Trigonometry as Logarithms: sech^-1(x)
0:07:33
Inverse Hyperbolic Functions using Log
0:08:58
Inverse hyperbolic functions and their logarithmic forms
0:12:48
Inverse Hyperbolic Functions as Logarithmic functions
0:07:34
Hyperbolic Functions: Definitions, Identities, Derivatives, and Inverses
0:32:32
Why don't they teach simple visual logarithms (and hyperbolic trig)?
0:07:01
Logarithmic Forms of Inverse Functions Expressing Cosine Hyperbolic Inverse Function in Logarithmic
0:24:18
The log form of Inverse Hyperbolic Functions.
0:05:47
A-Level Further Maths H4-03 Hyperbolic Inverse: Logarithmic Form of y=arcosh(x)
0:17:21
Logarithmic Forms of the Inverse Hyperbolic Functions
0:09:08
F3.1 3b Logarithmic form of inverse hyperbolic functions
0:10:12
Hyperbolic Trig Functions - Basic Introduction
0:04:52
Inverse tanh(x)
0:00:58
derivative of inverse hyperbolic sine | bprp calculus
0:12:48
Derivatives of Inverse Hyperbolic Functions
0:17:44
Inverse Hyperbolic Functions - Logarithmic Formula
0:04:22
A-Level Further Maths H4-01 Hyperbolic Inverse: Logarithmic Form of y=arsinh(x)
Комментарии