filmov
tv
Junior Math Olympiad Algebra Problem
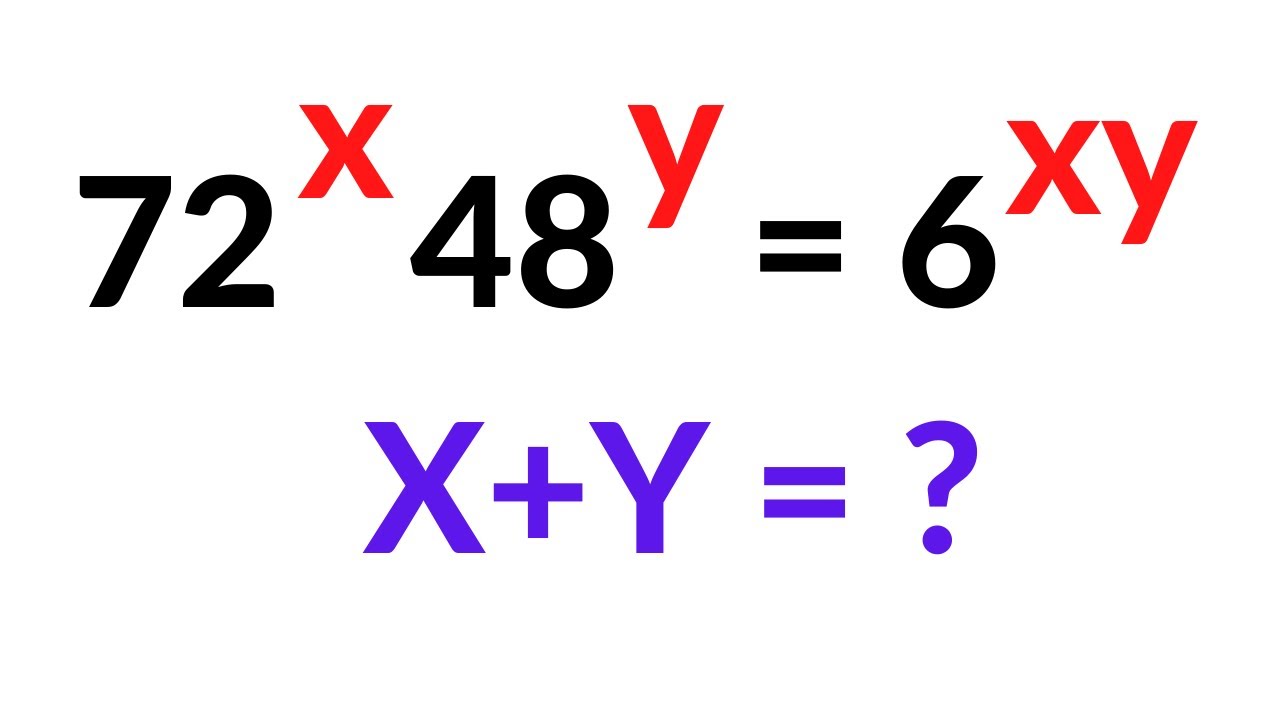
Показать описание
Junior Math Olympiad Algebra Problem
Maths Olympiad | A very tricky junior maths olympiad question | Algebra problems |
Junior Math Olympiad Algebra Problem
A Tricky Algebraic Maths Olympiad Questions Solutions | Junior Maths Olympiad |
Germany | Junior Maths Olympiad Questions | A nice algebra problem |
Olympiad Mathematics | Algebra Problem | Poland Junior Math Olympiad | Math Problems
Poland Junior Math Olympiad - Algebra Problem
Poland Junior Math Olympiad Problem - Algebra
Olympiad Mathematics - Algebra Problem | Vietnamese Junior Math Olympiad
Can You Solve This Math Olympiad Algebra Problem?║ Imo Exam Preparation
Olympiad Mathematics - Algebra | Poland Junior Math Olympiad Problem
Japanese l Very Nice Olympiad Math Tricky Problem l How to solve for x & y ??
Olympiad Mathematics | Algebra | Math Problems | Sweden Junior Math Olympiad
Ukrainian Junior Math Olympiad - Algebra Problem
Sweden Junior Math Olympiad Problem - Algebra
Olympiad Mathematics - A Nice Algebra Problem | Sweden Junior Math Olympiad
Romanian Junior Math Olympiad Problem - Algebra
Hungarian Junior Math Olympiad Problem - Algebra
Thailand Junior Math Olympiad Problem - Algebra
Junior Math Olympiad Algebra problem
Sweden Junior Math Olympiad Problem - Algebra
Japanese | Junior Maths Olympiad Questions | Algebra Problem |
Find the Value of X | Sweden Junior Math Olympiad Problem | Algebra
Junior Math Olympiad Question | A Nice Algebra Problem
Canadian Junior Math Olympiad Problem | Algebra | 2 Methods
Комментарии
 0:06:52
0:06:52
 0:04:43
0:04:43
 0:03:56
0:03:56
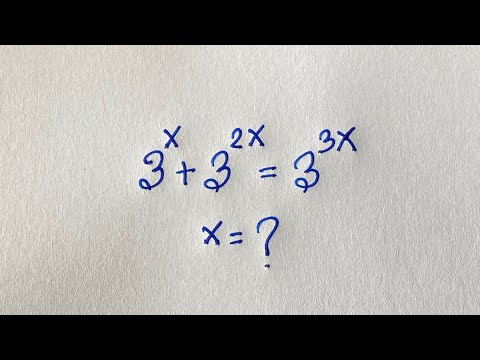 0:05:00
0:05:00
 0:03:27
0:03:27
 0:02:53
0:02:53
 0:02:08
0:02:08
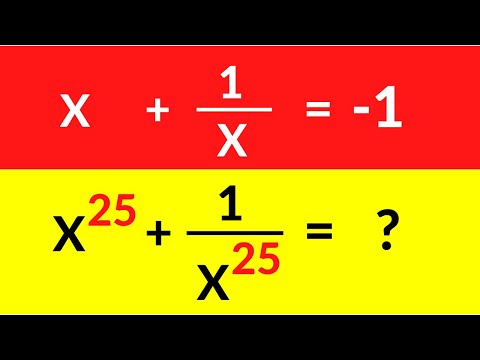 0:03:44
0:03:44
 0:06:06
0:06:06
 0:02:34
0:02:34
 0:13:49
0:13:49
 0:02:36
0:02:36
 0:01:49
0:01:49
 0:02:49
0:02:49
 0:02:37
0:02:37
 0:03:54
0:03:54
 0:03:33
0:03:33
 0:01:56
0:01:56
 0:09:43
0:09:43
 0:04:15
0:04:15
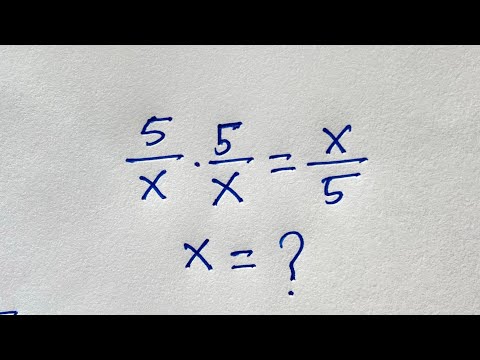 0:03:05
0:03:05
 0:05:54
0:05:54
 0:07:42
0:07:42
 0:08:23
0:08:23