Resonance on a string: fundamental frequency, linear density of a string example. Using v=f*lambda.

Resonance on a string: fundamental frequency, linear density of a string example. Using v=f*lambda.

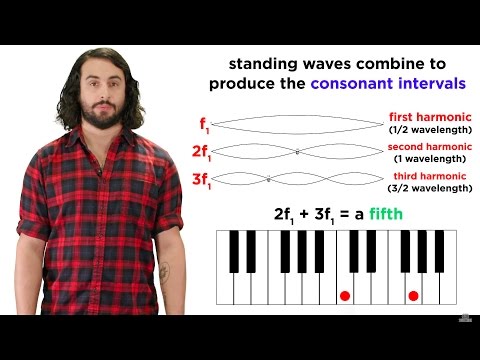
In this example, we are given a picture of the fourth harmonic on a string and told the frequency of the normal mode. We quickly review the pictures of standing waves for n=1, n=2, n=3 and n=4 to clarify that we are looking at the 4th harmonic. We count the antinodes in the standing wave and conclude we are looking at the fourth harmonic because the wave has four antinodes. Next, we apply f_n=nf_1 in order to solve for the fundamental frequency f_1. This is the frequency at which the standing wave would have only one antinode.

In the second part of the question, we find the linear density of the string. We start by finding the wave speed using v=f*lambda for the fourth harmonic. We determine the wavelength from the picture, and the wavelength is half the length of the string for this harmonic. Multiply wavelength and frequency, and we get the wave speed. Next, we state the formula relating speed, tension and linear density: v=sqrt(T/mu). We determine T using a force analysis of the hanging mass, then we solve for mu and plug in the numbers, obtaining a reasonable linear density for a light string.