filmov
tv
Solving the Dirac Equation | Any Frame (Hard Mode)

Показать описание
In this video, we will show you how to take the rest-frame solution of the Dirac equation and boost it to a general frame of reference.
Contents:
00:00 Introduction
00:20 Boost Matrix
00:44 Tedious Calculation
If you want to help us get rid of ads on YouTube, you can support us on Patreon!
Contents:
00:00 Introduction
00:20 Boost Matrix
00:44 Tedious Calculation
If you want to help us get rid of ads on YouTube, you can support us on Patreon!
L4.2 QED: Dirac Equation Solutions
Solving the Dirac Equation | Any Frame (Hard Mode)
Solving the Dirac Equation | Rest Frame
Solving the Dirac Equation | Any Frame (Easy Mode)
Quantum Field Theory Lecture 4: Finding Plane Wave Solutions to the Dirac Equation & Normalizati...
Solving the Impossible in Quantum Field Theory
Discovering the relativistic Dirac equation with Paul Dirac and graphene
How To Solve The Dirac Equation For The Hydrogen Atom | Relativistic Quantum Mechanics
Dirac Equation
L4.4 Dirac equation for the electron and hydrogen Hamiltonian
Spinor Normalization | Solving the Dirac Equation
Deriving The Dirac Equation
Solutions of the Dirac Equation
Quantum Mechanics 12a - Dirac Equation I
The Man Who Saved Quantum Physics When the Schrodinger Equation Failed
Negative Energy Solutions in the Dirac Equation | Dirac Sea VS. Feynman–Stueckelberg
The Dirac Equation - 4.3
Quantum Field Theory Lecture 3: Deriving the Dirac Equation (and gamma matrices!)
The Equation That Explains (Nearly) Everything!
Dirac equation: particles and fields
Dirac Equation | Derivation and Introduction
Plane Wave Solutions To The Dirac Equation | Relativistic Quantum Mechanics
The Schrödinger Equation Explained in 60 Seconds
How did Dirac discover the Dirac Equation #Shorts
Комментарии
 0:06:04
0:06:04
 0:03:23
0:03:23
 0:06:13
0:06:13
 0:03:56
0:03:56
 0:53:44
0:53:44
 0:15:21
0:15:21
 0:29:06
0:29:06
 0:37:09
0:37:09
 0:50:01
0:50:01
 0:15:01
0:15:01
 0:04:11
0:04:11
 0:23:40
0:23:40
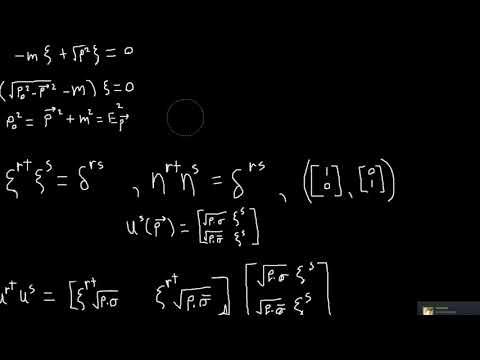 0:07:55
0:07:55
 0:17:06
0:17:06
 0:12:57
0:12:57
 0:05:09
0:05:09
 0:12:35
0:12:35
 0:48:17
0:48:17
 0:16:43
0:16:43
 0:47:10
0:47:10
 0:04:26
0:04:26
 0:07:52
0:07:52
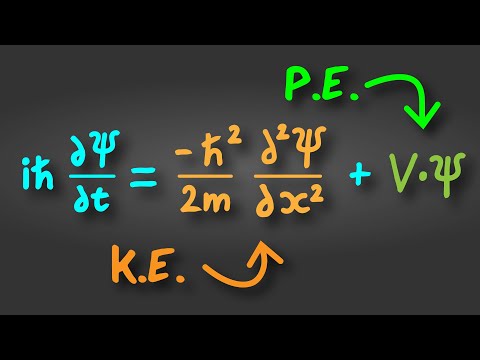 0:01:00
0:01:00
 0:01:00
0:01:00