filmov
tv
How to Find the Remainder | Number Theory

Показать описание
How to Find the Remainder | Number Theory
Join this channel to get access to perks:
Topics covered in this video
what is remainder theory
the concept of negative remainder
remainder theorem in number system
remainder theorem
remainder
number theory
michael penn
mathematics
math
how to find the remainder - number theory
how to find remainders easily
how to find remainders
find the remainder with the help of congruence
find the remainder
fermat’s little theorem
division
abstract algebra
Join this channel to get access to perks:
Topics covered in this video
what is remainder theory
the concept of negative remainder
remainder theorem in number system
remainder theorem
remainder
number theory
michael penn
mathematics
math
how to find the remainder - number theory
how to find remainders easily
how to find remainders
find the remainder with the help of congruence
find the remainder
fermat’s little theorem
division
abstract algebra
How to Calculate the Remainder : Number Theory Education
[Old SAT] Finding Remainders With Your Calculator - Reason Prep Daily #4
Introduction to remainders
Aptitude Made Easy - Find the Remainder in seconds, Math Tricks, Shortcuts, Basics and Methods
Long Division with Remainder | Easy Example
If (27)^999 is divided by 7, then the remainder is:
Quick and Easy Way to Find the Remainder of a Polynomial - Use the Remainder Theorem!
How to Find the Remainder | Number Theory
How to find Remainder/Mod with or without Calculator
Find Modulus or remainder of a number using scientific calculator.
Remainder Theorem and Synthetic Division of Polynomials
Remainder & Factor Theorem (1 of 2: How do we calculate remainders without dividing?)
Find a Remainder Using Congruences: 2^(124)/7
Remainder Theorem by Long Division
How to Find the Remainder of a Polynomial - When Divisor has a Leading Coefficient other than ONE
The Remainder Theorem - How to Find the Remainder when Dividing Polynomials?
How to Find the Remainder and Quotient when Dividing Integers
How to Find the Remainder With the Help of Congruence | Number Theory
How to find the remainder of a division problem in Excel
How to find remainder of a number with power #fastandeasymaths #math #mathematics #remainder #like
Japanese Method #shorts
Find the Quotient and Remainder When Dividing Numbers
Number System || Finding Remainder ? (LESSON-4)
(MATH) How To Divide Numbers With Remainder? | #iQuestionPH
Комментарии
 0:01:46
0:01:46
![[Old SAT] Finding](https://i.ytimg.com/vi/9NYsEMbt4Ag/hqdefault.jpg) 0:04:32
0:04:32
 0:04:49
0:04:49
 0:05:34
0:05:34
 0:01:00
0:01:00
 0:00:29
0:00:29
 0:03:58
0:03:58
 0:04:51
0:04:51
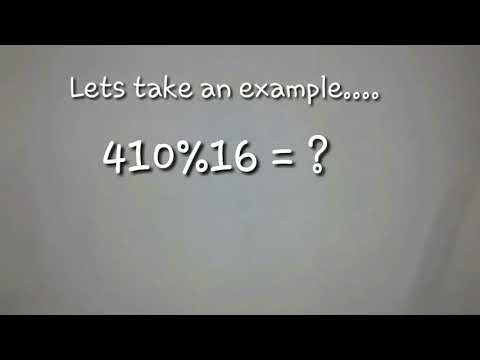 0:00:53
0:00:53
 0:00:44
0:00:44
 0:10:34
0:10:34
 0:08:39
0:08:39
 0:02:39
0:02:39
 0:02:37
0:02:37
 0:06:17
0:06:17
 0:13:46
0:13:46
 0:01:53
0:01:53
 0:03:43
0:03:43
 0:01:52
0:01:52
 0:06:16
0:06:16
 0:00:20
0:00:20
 0:02:58
0:02:58
 0:29:33
0:29:33
 0:08:20
0:08:20