filmov
tv
Symmetric Matrices and Positive Definiteness

Показать описание
MIT 18.06SC Linear Algebra, Fall 2011
Instructor: David Shirokoff
A teaching assistant works through a problem on symmetric matrices and positive definiteness.
License: Creative Commons BY-NC-SA
Instructor: David Shirokoff
A teaching assistant works through a problem on symmetric matrices and positive definiteness.
License: Creative Commons BY-NC-SA
Symmetric Matrices and Positive Definiteness
Checking if a Matrix is Positive Definite
How to Prove that a Matrix is Positive Definite
5. Positive Definite and Semidefinite Matrices
A Criterion for Positive Definiteness of a Symmetric Matrix
Positive Definite Matrices and Minima
Positive Definite Matrices
Positive definite matrix|2 by 2 real symmetric matrix| Linear Algebra
What Does It Mean For a Matrix to be POSITIVE? The Practical Guide to Semidefinite Programming(1/4)
Eigenvectors of Symmetric Matrices Are Orthogonal
Vector Calculus 14: The Dot Product Matrix Is Positive Definite
How to Prove A Symmetric Positive Definite Matrix (SPD)
For a Positive Definite M, Is BᵀMB Always Positive Definite, Too?
Simple proof that any covariance matrix is positive semi-definite
2.7.5 Positive Definite Matrices & The Five Classes of Symmetric Matrix
Test 1 Positive and Negative Definite or Semi Definite Matrix With Example
Lecture 3 Special types of symmetric matrices | Positive Definite | Negative Definite | Indefinite
Positive semidefinite matrix-example.
Positive Definite Matrices
Positive-Definite Matrix
The LDU and LDLᵀ Decompositions and the Implications for Positive Definiteness
IMA ECM Spring 2021 - Completing, Thresholding & Factorizing Symmetric Positive Definite Matrice...
Positive Definite Matrices Video Lecture
Extra Problems 1.5-1.7 Positive Definite Matrices
Комментарии
 0:12:40
0:12:40
 0:02:06
0:02:06
 0:06:52
0:06:52
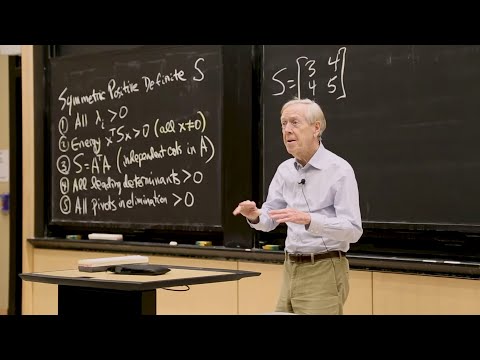 0:45:27
0:45:27
 0:16:19
0:16:19
 0:12:50
0:12:50
 0:21:41
0:21:41
 0:02:35
0:02:35
 0:10:10
0:10:10
 0:11:28
0:11:28
 0:11:05
0:11:05
 0:15:56
0:15:56
 0:05:27
0:05:27
 0:05:58
0:05:58
 0:19:18
0:19:18
 0:05:20
0:05:20
 0:07:05
0:07:05
 0:04:49
0:04:49
 0:12:43
0:12:43
 0:03:03
0:03:03
 0:18:18
0:18:18
 0:44:13
0:44:13
 0:43:25
0:43:25
 0:12:28
0:12:28