filmov
tv
5. Positive Definite and Semidefinite Matrices

Показать описание
MIT 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning, Spring 2018
Instructor: Gilbert Strang
In this lecture, Professor Strang continues reviewing key matrices, such as positive definite and semidefinite matrices. This lecture concludes his review of the highlights of linear algebra.
License: Creative Commons BY-NC-SA
Instructor: Gilbert Strang
In this lecture, Professor Strang continues reviewing key matrices, such as positive definite and semidefinite matrices. This lecture concludes his review of the highlights of linear algebra.
License: Creative Commons BY-NC-SA
5. Positive Definite and Semidefinite Matrices
Checking if a Matrix is Positive Definite
Positive Definite Matrices and Minima
How to Prove that a Matrix is Positive Definite
Test 5 For Positive and Negative Definite or Semi-Definite Matrix with Example | Symmetric Matrix
Test 1 Positive and Negative Definite or Semi Definite Matrix With Example
What Does It Mean For a Matrix to be POSITIVE? The Practical Guide to Semidefinite Programming(1/4)
Positive Definite Matrices
Symmetric Matrices and Positive Definiteness
2.7.5 Positive Definite Matrices & The Five Classes of Symmetric Matrix
How to check positive definite and positive semidefinite matrix
Positive semidefinite matrix-example.
Lec 5 Positive definite matrices
Five Tests For Positive and Negative Definite or Semi Definite Matrix | Types of Matrices
Positive Definite,Positive SemiDefinite,NegativeDefinite,Negative SemiDefinite,Indefinite Matrix
Lecture 3 Special types of symmetric matrices | Positive Definite | Negative Definite | Indefinite
Advanced Linear Algebra 20: Positive Definite & Positive Semidefinite Matrices
Types of Matrix- Positive definite, Semi definite & Negative definite, Practical |MultiDOF3|Vib|...
Test 3 Positive and Negative Definite or Semi-Definite Matrix with Example
The Practical Guide to Semidefinite Programming (2/4)
💥Positive Definite💥indefinite 🌟Trick Based
For a Positive Definite M, Is BᵀMB Always Positive Definite, Too?
Simple proof that any covariance matrix is positive semi-definite
A practical way to check if a matrix is positive-definite (5 Solutions!!)
Комментарии
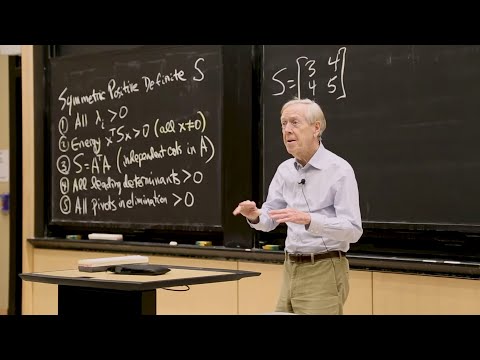 0:45:27
0:45:27
 0:02:06
0:02:06
 0:12:50
0:12:50
 0:06:52
0:06:52
 0:06:17
0:06:17
 0:05:20
0:05:20
 0:10:10
0:10:10
 0:21:41
0:21:41
 0:12:40
0:12:40
 0:19:18
0:19:18
 0:04:31
0:04:31
 0:04:49
0:04:49
 0:25:39
0:25:39
 0:08:33
0:08:33
 0:04:02
0:04:02
 0:07:05
0:07:05
 0:46:28
0:46:28
 0:06:03
0:06:03
 0:05:43
0:05:43
 0:07:26
0:07:26
 0:00:06
0:00:06
 0:05:27
0:05:27
 0:05:58
0:05:58
 0:04:03
0:04:03