filmov
tv
Using prime factorization to simplify the square root of an expression

Показать описание
👉 Learn how to simplify the square root of an expression. The square root of an expression is an expression which will multiply itself twice to give the original expression. To simplify the square root of an expression, we decompose/factor the expression into a product of two terms that are the same. The term of the product is the required square root.
When the radical cannot be conveniently decomposed/factored into two same terms, we factor the radicand into a product of a perfect square and a non-perfect square. Using the product/quotient rule of radicals the perfect square is evaluated and the non-perfect square is left as a radical.
Organized Videos:
✅How To Simplify a Radical Expression
✅How To Simplify The Cube Root of a Number
✅How to Simplify The 4th Root of a Number
✅How to Simplify the Square Root of a Number
✅How to Simplify The Square Root of a Number with Coefficient
✅How to Simplify Expressions | 4th Root
✅How to Simplify Radical Expressions | 5th Root
✅How to Simplify Radical Expressions | Cube Root
✅How to Simplify Radical Expressions | Learn About
✅How to Simplify Radical Expressions | Easy
✅How to Simplify Radical Expressions | Hard
Connect with me:
#Simplifyradicals #radicals #brianmclogan
When the radical cannot be conveniently decomposed/factored into two same terms, we factor the radicand into a product of a perfect square and a non-perfect square. Using the product/quotient rule of radicals the perfect square is evaluated and the non-perfect square is left as a radical.
Organized Videos:
✅How To Simplify a Radical Expression
✅How To Simplify The Cube Root of a Number
✅How to Simplify The 4th Root of a Number
✅How to Simplify the Square Root of a Number
✅How to Simplify The Square Root of a Number with Coefficient
✅How to Simplify Expressions | 4th Root
✅How to Simplify Radical Expressions | 5th Root
✅How to Simplify Radical Expressions | Cube Root
✅How to Simplify Radical Expressions | Learn About
✅How to Simplify Radical Expressions | Easy
✅How to Simplify Radical Expressions | Hard
Connect with me:
#Simplifyradicals #radicals #brianmclogan
 0:02:37
0:02:37
 0:05:16
0:05:16
 0:03:20
0:03:20
 0:02:36
0:02:36
 0:09:45
0:09:45
 0:02:09
0:02:09
 0:08:46
0:08:46
 0:05:37
0:05:37
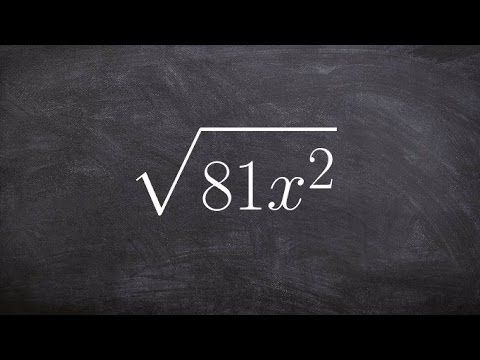 0:01:07
0:01:07
 0:06:26
0:06:26
 0:02:28
0:02:28
 0:08:44
0:08:44
 0:06:40
0:06:40
 0:03:59
0:03:59
 0:02:27
0:02:27
 0:01:45
0:01:45
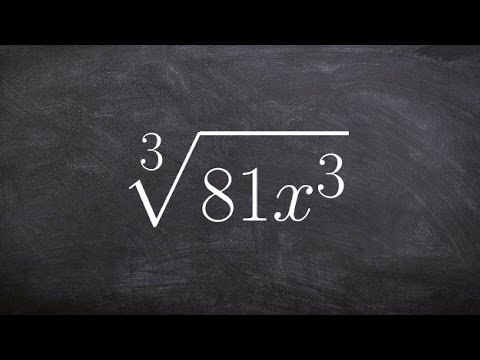 0:01:43
0:01:43
 0:08:31
0:08:31
 0:02:54
0:02:54
 0:03:46
0:03:46
 0:00:46
0:00:46
 0:10:57
0:10:57
 0:07:31
0:07:31
 0:02:13
0:02:13