filmov
tv
Why does integrating the function of a curve give you the area under the curve?

Показать описание
You have probably been taught that if you want to find the area under a function / line, you will integrate the equation of the line. But why is it that when you integrate the equation of the line, you get the area underneath the line? Here is a full explanation. p.s. You will need to know basic limits and how to differentiate using first principles.
What is Integration? 3 Ways to Interpret Integrals
What is integration? This video explains the concept of integration #calculus #integration
Calculus: Why does integrating a function give area under its curve?
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
This is all Integration is (quickfire AI lesson)
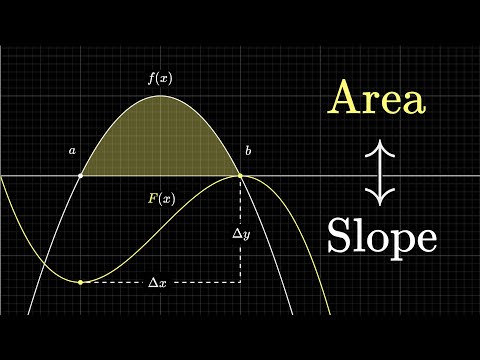
What does area have to do with slope? | Chapter 9, Essence of calculus
So what is integration?
How REAL Men Integrate Functions
Project | APIHUB in React JS ⚡ | Part 2 | React 2025
Integral explained😮 | integration
Integration rundown by Goggins (quick AI lesson)
Understanding Calculus in One Minute... 🤯
Calculus Explained In 30 Seconds
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
What is Integration? Finding the Area Under a Curve
Integration (Calculus)
Integration Using The Substitution Rule
Why integration gives area
derivative vs integral
Why do logarithmic functions have absolute value signs after integration?
Integration by substitution (visualised)
Why Do We Use a Constant After Integrating an Indefinite Integral? #Shorts #calculus #math #learn
integration by parts is easy
The definition of a derivative
Комментарии
 0:10:55
0:10:55
 0:00:44
0:00:44
 0:09:36
0:09:36
 0:20:46
0:20:46
 0:00:59
0:00:59
 0:12:39
0:12:39
 0:04:00
0:04:00
 0:00:35
0:00:35
 0:26:46
0:26:46
 0:00:22
0:00:22
 0:00:44
0:00:44
 0:00:52
0:00:52
 0:00:45
0:00:45
 0:00:09
0:00:09
 0:08:18
0:08:18
 0:07:04
0:07:04
 0:10:40
0:10:40
 0:03:32
0:03:32
 0:00:12
0:00:12
 0:05:09
0:05:09
 0:07:42
0:07:42
 0:00:38
0:00:38
 0:00:33
0:00:33
 0:01:00
0:01:00