filmov
tv
A continuous function equation.

Показать описание
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
A continuous function equation.
3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus
Defining a function at a point to make it continuous | Limits | Differential Calculus | Khan Academy
Continuity and Differentiability EXPLAINED with Examples
Continuity and Differentiability
Continuity - 2 Examples
Find the values a and b that make the piecewise function continuous
Calculus - Continuous functions
Yudovich Theory for Rough path Perturbations of Euler’s Equation (Lecture 4) by Torstein Nilssen
Continuous, Discontinuous, and Piecewise Functions
Continuity Basic Introduction, Point, Infinite, & Jump Discontinuity, Removable & Nonremovab...
Find the value makes a piecewise function continuous with system of equations
Find the value k that makes the function continuous
Piecewise Functions - Limits and Continuity | Calculus
How to determine if a function is continuous and differentiable
Continuous function: an example / tutorial
Determine if the Piecewise Function is Continuous by using the Definition of Continuity
Determine the discontinuity of the function
What is continuity?
Learn how to determine if a piecewise function is continuous and differentiable
A Continuous Functional Equation
Example: When is a Piecewise Function Continuous?
Determine if a piecewise function is continuous or discontinuous
Continuity on an Interval
Комментарии
 0:06:19
0:06:19
 0:10:10
0:10:10
 0:04:57
0:04:57
 0:05:33
0:05:33
 0:32:48
0:32:48
 0:11:08
0:11:08
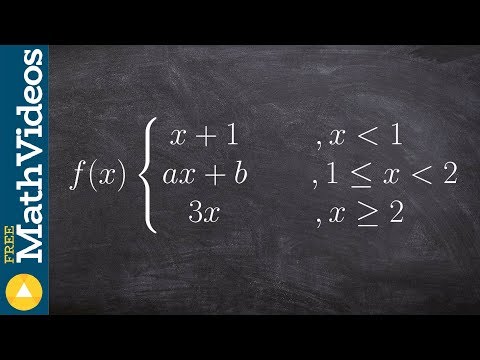 0:03:44
0:03:44
 0:08:45
0:08:45
 1:41:31
1:41:31
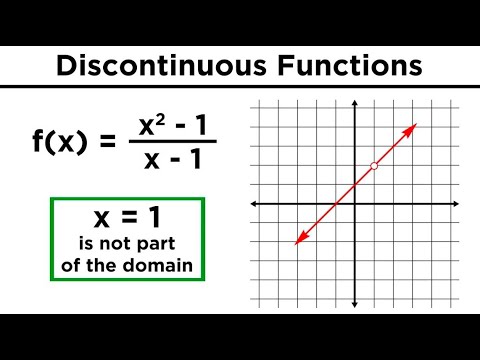 0:05:18
0:05:18
 0:13:31
0:13:31
 0:07:00
0:07:00
 0:02:50
0:02:50
 0:10:06
0:10:06
 0:02:21
0:02:21
 0:07:42
0:07:42
 0:04:01
0:04:01
 0:01:05
0:01:05
 0:04:32
0:04:32
 0:02:37
0:02:37
 0:10:36
0:10:36
 0:03:18
0:03:18
 0:01:45
0:01:45
 0:13:36
0:13:36