How to solve the Diophantine equation xyz = xy + yz + zx?

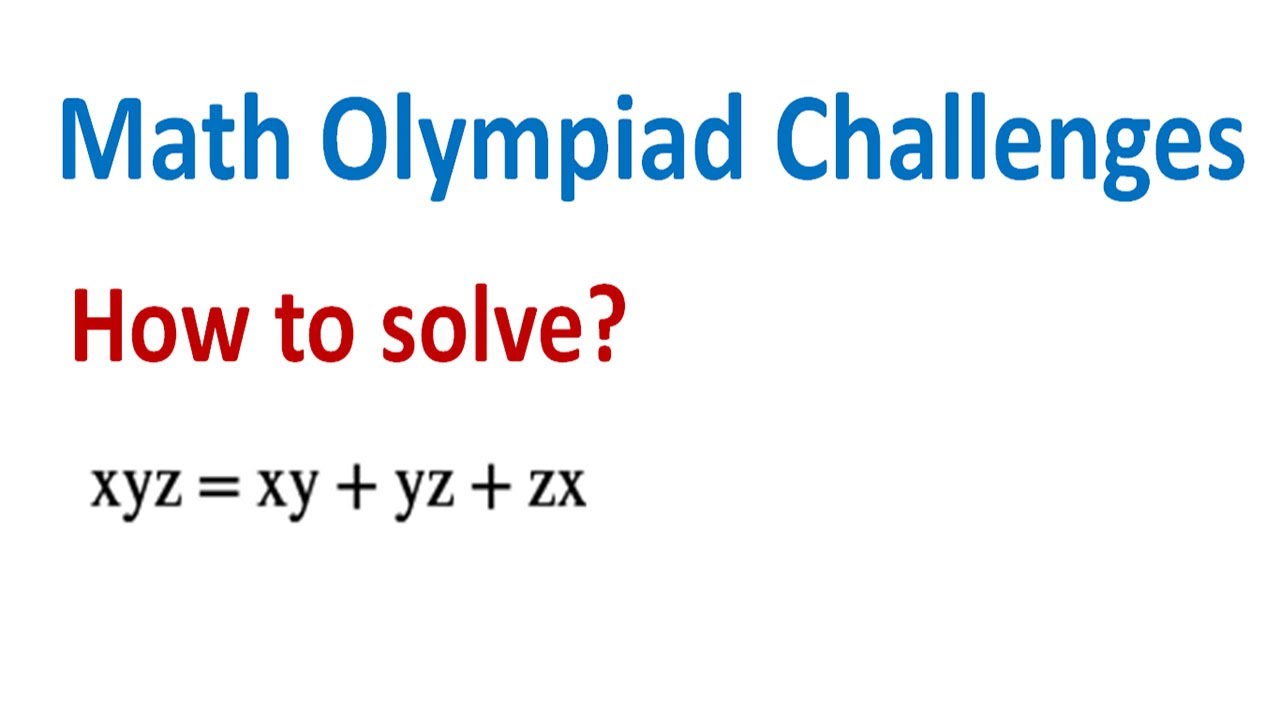
Показать описание

The video illustrates step-by-step how to solve the Diophantine equation xyz = xy + yz + zx.
As x, y and z are positive integers, so x, y, z≠0. By dividing both sides of the original equation, we have 1=1/x+1/y+1/z. The next step is to narrow down the range of possible integers, for example, by assuming x ≥ y ≥ z.

Subscribe at:

#MathsEnhancer #MathematicalCompetition #MathematicalOlympiad #ChallengingMathematicsProblems #MathematicsCompetition #EnhanceMathematicsProblemSolvingSkills #Mathematics
#ImproveMathematicsGrades
Solve the Diophantine equations
Find integer solutions of equations
Challenging mathematics problems
Enhance mathematics problem solving skills
Mathematical competition questions
Mathematics competition questions
Improve mathematics grades
Olympics math
Olympics maths
Olympics mathematics
Olympics math competition
Math Olympiad training
International Mathematical Olympiad questions and solutions
International Mathematical Olympiad questions and answers
How to solve Olympiad question
How to solve International Mathematical Olympiad question
How to solve Olympiad Mathematics Question
How to prepare for Maths Olympiad
How to prepare for Math Olympiad
Olympiad mathematics competition
Olympiad exam
Olympiad exam sample paper
Maths Olympiad sample question
Maths Olympiad sample answer
Math Olympiad

Maths Enhancer's Class

Рекомендации по теме

Комментарии

Nice problems and well explained.
For the additional problem, (a, b, c, d)=(42, 7, 3, 2), (24, 8, 3, 2), (18, 9, 3, 2), (15, 10, 3, 2), (12, 12, 3, 2) and many others.

markkerbyson

I miss to write conditions for one of the problems in the last comment. Regarding "Q4-(10)",
a+b+c+d+e = a^3+b^3+c^3+d^3+e^3 = 5 (a, b, c, d, e: integers) (a≧b≧c≧d≧e)
Find all (a, b, c, d, e). Find more than 6 solutions. (If there are less than 6 solutions, prove it.)
is the correct problem. The condition (a≧b≧c≧d≧e) was omitted. [ Excuse me. ]

sy

For the additional problem, there are too many solutions. I list a few example solutions (a, b, c, d)=(8, 8, 4, 2), (12, 6, 4, 2), (20, 5, 4, 2)

kkyoung

How to solve the Diophantine equation xyz = xy + yz + zx?

A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad

Diophantine Equations: Strategies and Examples

Diophantine Equation: ax+by=gcd(a,b) ← Number Theory

Solve Diophantine Equations by Factoring

Number Theory | Linear Diophantine Equations

Solving Linear Diophantine Equations - Simplified

A Linear Diophantine Equation

How to Solve a Three Variable Linear Diophantine Equation

How To Solve Linear Diophantine Equations

Diophantine Equations with 1 Variable ← Number Theory ← Socratica

A Linear Diophantine Equation

Linear Diophantine Equations with 3 Variables - 3 Different Methods

Diophantine Equation | Integer Solutions?

A Special Diophantine Equation in Number Theory with Special Formula You Need to Master

A Complete Guide To Solving Linear Diophantine Equations - Part One

How to Solve a Diophantine Equation | Integer Solutions?

Cool Algebraic Tricks! | How to Solve the Quadratic Diophantine Equation?

Introduction to Solving Linear Diophantine Equations Using Congruence

How to Solve the Diophantine Equation?

Solve Diophantine Equation by Factoring

Solving a Quadratic Diophantine Equation

Solve and Check | Learn how to solve the Diophantine Equation fast | Math Olympiad Preparation

Solving a Diophantine Equation by Factoring | Solve for Integer Solutions #NumberTheory

A Linear Diophantine Equation | 3x+4y=17