filmov
tv
Maximum sum of consecutive differences circular array | Max product subset | Love Babbar DSA sheet

Показать описание
A great E-book on Data structures and algorithms written by a software engineer who has himself worked in MNC's. Its available for a very affordable price.
Do check it out by clicking on the link below and boost your preparation.
Problems and solutions:
1.Maximum sum of consecutive differences in a circular array:
solution:
2.Maximum product subset of array:
Playlist link:
Link to the questions:
Connect with me on Linkedin:
Connect with me on instagram:
#LoveBabbardsasheet #greedy #dsa #Placement #Coding #Fun #SDE #GFG #greedy #sorting
Do check it out by clicking on the link below and boost your preparation.
Problems and solutions:
1.Maximum sum of consecutive differences in a circular array:
solution:
2.Maximum product subset of array:
Playlist link:
Link to the questions:
Connect with me on Linkedin:
Connect with me on instagram:
#LoveBabbardsasheet #greedy #dsa #Placement #Coding #Fun #SDE #GFG #greedy #sorting
Maximize sum of consecutive differences in a circular array | Greedy | GFG Problem | MAANG Problem
Maximum sum of consecutive differences circular array | Max product subset | Love Babbar DSA sheet
Kadanes algorithm | Longest sum contiguous subarray
Finding Maximum Sum SubArray using Divide and Conquer Approach.
The sum of 3 consecutive numbers is 150. Find the difference between the largest and smallest number
Sum of consecutive even numbers. #shorts #mathstricks
Kadane's Algorithm | Largest Sum Contiguous Subarray | Java and C++ | Anuj Bhaiya ✅DSAOne Cours...
'Array Max Consecutive Sum' - Codesignal #37 - JAVA Solution
If sum of two consecutive numbers are 121, what are the numbers?
Dp 16. Partition A Set Into Two Subsets With Minimum Absolute Sum Difference | DP on Subsequences
Adding Consecutive Numbers Math Trick I Number Series Problems
Have You Ever Noticed This About Consecutive Numbers? #shorts
Find 3 Consecutive Even Integers with a Sum of 72
Excel: Sum Across Multiple Columns With One or More Criteria - 3 Methods
2 Sum Problem | 2 types of the same problem for Interviews | Brute-Better-Optimal
DP 5. Maximum Sum of Non-Adjacent Elements | House Robber | 1-D | DP on Subsequences
Lecture 105: Maximum Sum of Non-Adjacent Elements || DP Series
#trick26 ,sum of consecutive numbers
The average of 7 consecutive numbers is 20. The largest of these numbers is.#shorts
Subarray sum equals K | Number of subarrays with sum equals K | Leetcode #560
The average of five consecutive odd numbers is 61. What is the difference between the highest and
Sum of consecutive even number starting from 2. #shorts #mathstricks
Find the sum of first n squares, difference equation approach, (ft. Max!)
LeetCode 967. Numbers With Same Consecutive Differences
Комментарии
 0:06:52
0:06:52
 0:15:31
0:15:31
 0:07:51
0:07:51
 0:10:22
0:10:22
 0:02:43
0:02:43
 0:00:14
0:00:14
 0:14:02
0:14:02
 0:07:25
0:07:25
 0:01:54
0:01:54
 0:29:50
0:29:50
 0:01:17
0:01:17
 0:00:55
0:00:55
 0:01:36
0:01:36
 0:04:53
0:04:53
 0:18:20
0:18:20
 0:32:23
0:32:23
 0:20:33
0:20:33
 0:00:11
0:00:11
 0:00:09
0:00:09
 0:15:44
0:15:44
 0:01:20
0:01:20
 0:00:15
0:00:15
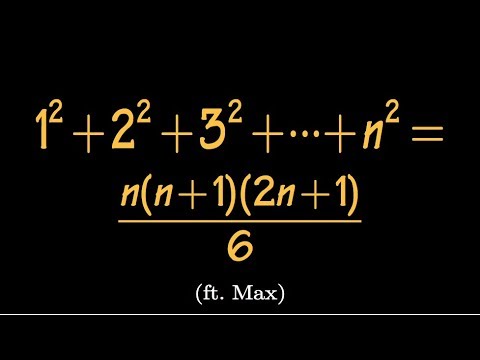 0:11:19
0:11:19
 0:11:38
0:11:38