Vector Equation of Line of Intersection of Two Planes

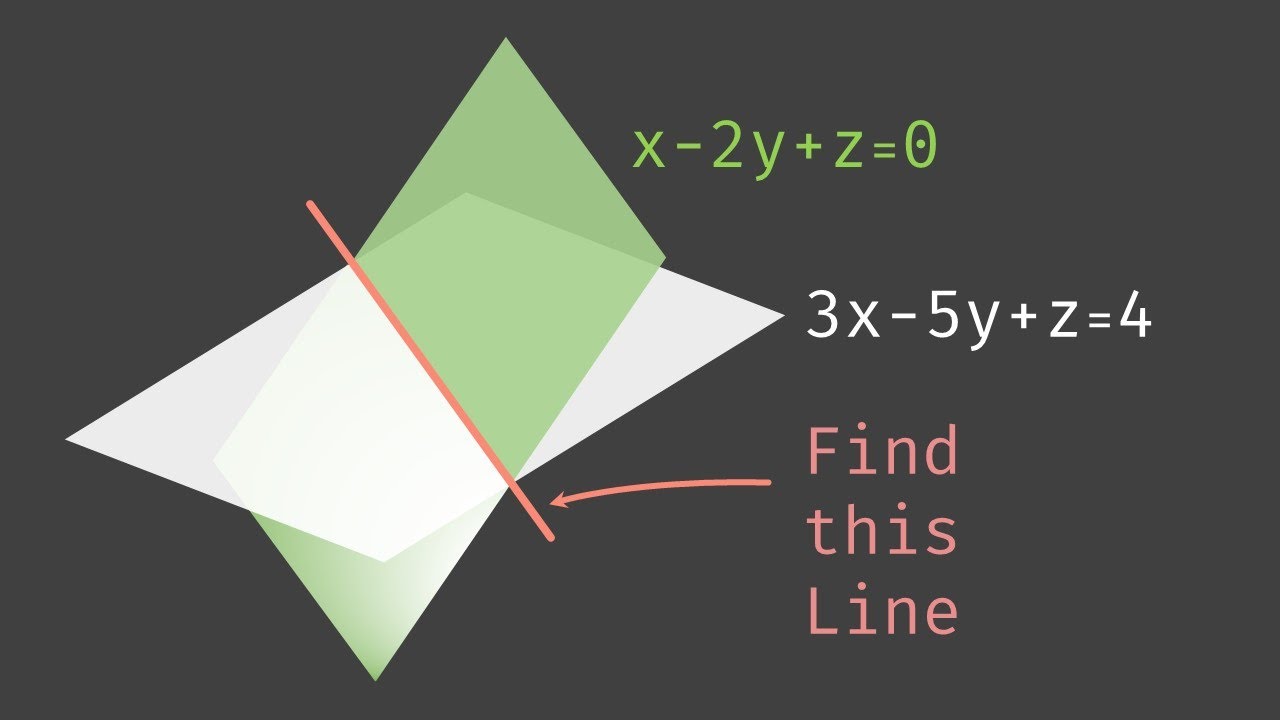
How do we find a vector equation of line of intersection of two planes x-2y+z=0 and 3x-5y+z=4? We first want to find two points on the line of intersection, and the two points must lie on the plane. After that, we can use the two points to find the direction vector of the line, then use one of the points to write down the parametrization.

📺 Subscribe to my channel for Math Learning!

Please help me by subscribing to my YouTube channel. I want to use my free time to make a lot of math videos to help others and to make education available to the world. Your sharing and subscribing will help this channel be reached by more people. Thank you!

Follow me:

Ayúdame suscribiéndome a mi canal de YouTube. Quiero usar mi tiempo libre para hacer muchos videos de matemáticas para ayudar a otros y hacer que la educación esté disponible para el mundo. Tus Me gusta y Suscripciones ayudarán a que más personas lleguen a este canal. ¡Gracias!

請訂閱我的YouTube Channel, 我會製作更多與數學相關的視頻，讓世界各地的朋友用簡單的方法學習數學（數學考試一定A）！請用您的訂閱和點贊支持我，並在留言區與我討論！謝謝！

#Geometry #Calculus #Math

[bluekeenhd]

if you have two equations that do not cancel out a number, can you multiply one equation by a constant (on both sides) to cancel out a variable?
Ex: eq1 --> -x-3y-4z = 2
eq2 --> 2x + 2y +2z = 5

[Ppooh]

i used a random y value to get point B and when i subtracted B-A to get the vector, it did not match to method 2. I used fractions and i am certain i havent miscalculated. What may be the issue then? great video by the way

[arjunarun]

Great video, just wanted to say if two lines aren't parallel it doens't mean they must intersect (0:52-1:00)

[erickpascual-bautista]

hey I have a question so I understand approach two how when you cross them you get a vector perpendicular to the two norm vectors of my plane which result in the direction vector of the line of intersection, however where do I get my point from? since you need a direction vector and a point on the line to create the vector equation. do I just use the norm vector as one of my points
so norm vector 1 was <3, -5, 1>
so my equation would be
<3, -5, 1> + <-3, -2, -2>t
then obviously multiply it out if you want the parametric form

[Alborzhakimi]

hello, thank you for your video. I had a question regarding your first approach. I already used your second approach and then attempted to check my answer for V by using the first approach. However, the Z did not cancel out so I had to multiply the equation of the second plane by -2 to get the Z to cancel. Next, I proceeded with your approach and got 2 points and subtracted them from each other. However, the answer did not end up the same as the answer of V with the first approach. Do you have any idea why this is? I could send you a picture of my work so you could check it out, if you would like. Thanks for your time.

[marthamaywhovier]

Does it matter which one of the planes I subtract ?

[jimmmy]

so am i free to pick whichever number ?

[wackaflacka]

Didn't much like the video, not enough explanation. Needed approach 2, but everything was super fast forwards, expecially with the n1 (multiplication sign) n2. I mean I understood it because I knew how to do it, but for the people that don't?

[richardsdiana]

Can I give a vector equation for the intersection between the two planar equations?