filmov
tv
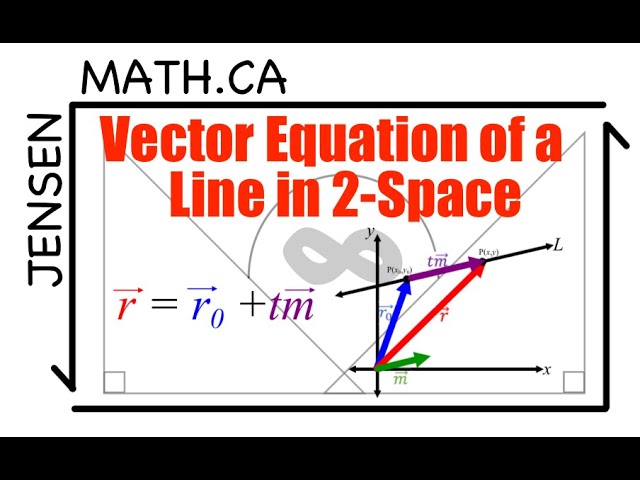
Vector Equation of a Line in 2-space (full lesson) | MCV4U
Показать описание
How To Find The Vector Equation of a Line and Symmetric & Parametric Equations
The Vector Equation of Lines | Multivariable Calculus
Vector Equation of a Line
Finding the Vector Equation of a Line
The Vector Equation of a Line
Vector Equation of a Line (1 of 2: Lines in 3 dimensions)
Vector Equation of a Line [IB Math AA HL]
Vector and Parametric Equations of a Line (Line in 3 dimensions)
Assertion (A): The vector equation of a line passing through the points \\(\\mathrm{A}(-1,0,2)\\....
A-Level Further Maths F1-01 Lines: Introducing the Vector Equation of a Line
Vector Equation of Line Through Two Points Q2
Vector Equation of a Line in 2-space (full lesson) | MCV4U
How to find the vector equation of a line
Vector Equation of Line Segment Concept
Vector Equations of Lines
How To Find The Equation of a Plane Given a Point and Perpendicular Normal Vector
Parametric representations of lines | Vectors and spaces | Linear Algebra | Khan Academy
Intro to the vector equation of a line in 2D or 3D - IB Math SL
Vector Equation of a line in 2D
Class 12th – Vector Equation of Line Passing Through 1 Point | Tutorials Point
12.5: Equations of Lines & Planes (1/2)
Vector and parametric equations of a line
Vector Equation of a Line [IB Math AI HL]
How to find the vector equation of a line, Derivation and example
Комментарии
 0:11:37
0:11:37
 0:05:30
0:05:30
 0:16:45
0:16:45
 0:07:41
0:07:41
 0:05:30
0:05:30
 0:11:11
0:11:11
 0:06:12
0:06:12
 0:13:38
0:13:38
 0:04:43
0:04:43
 0:07:01
0:07:01
 0:01:19
0:01:19
 0:32:28
0:32:28
 0:05:55
0:05:55
 0:08:53
0:08:53
 0:11:16
0:11:16
 0:07:37
0:07:37
 0:24:46
0:24:46
 0:07:31
0:07:31
 0:04:18
0:04:18
 0:01:37
0:01:37
 0:41:21
0:41:21
 0:03:51
0:03:51
 0:06:22
0:06:22
 0:08:04
0:08:04