filmov
tv
Hausdorff Example 3: Function Spaces

Показать описание
Point Set Topology: For a third example, we consider function spaces. We begin with the space of continuous functions on [0,1]. As a metric space, this example is Hausdorff, but not complete. We consider Cauchy sequences and a possible completion.
Hausdorff Example 3: Function Spaces
Hausdorff Example 2: Quotient Space
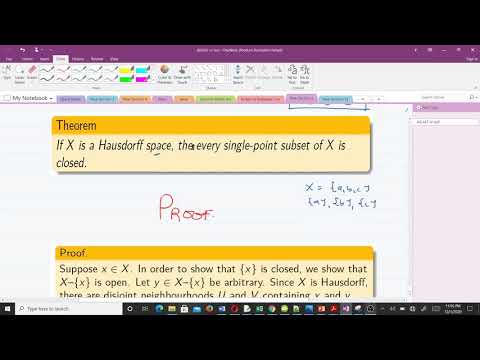
Hausdorff topological spaces
Intuitive Topology 7: Hausdorff
Manifolds 3 | Hausdorff Spaces [dark version]
Hausdorff Spaces
Hausdorff spaces
Hausdroff Space | Examples | Topological Space | Higher mathematics | Ravina Tutorial
T1 – Spaces and Hausdorff Spaces - Chapter1videoLec-4
Topology Lecture 07: Hausdorff Spaces
Hausdorff Space
Hausdorff spaces - Properties with proofs | Topology
Hausdorff Example 1: Cofinite Topology
Diagonal of a set & Hausdorff spaces
General Topology Lec03 Closed sets, limit points and Hausdorff Spaces
2020 Hausdorff School on p4est/3: Algorithms
Separated and Hausdorff
Metric Spaces | Lecture 36 | Hausdorff Property
Hausdorff space
Hausdorff spaces | Wikipedia audio article
Hausdorff space | Wikipedia audio article
MAST30026 Lecture 11: Hausdorff spaces (Part 3)
Define a Hausdorff space. Give it example. prove that every discrete space is hausdroff #part3 #BSC
Hausdorff Meaning
Комментарии
 0:14:55
0:14:55
 0:06:03
0:06:03
 0:16:05
0:16:05
 0:13:52
0:13:52
 0:09:11
0:09:11
 0:10:36
0:10:36
 0:05:12
0:05:12
 0:13:33
0:13:33
 0:51:36
0:51:36
 0:32:01
0:32:01
 0:09:56
0:09:56
 0:14:26
0:14:26
 0:09:21
0:09:21
 0:17:14
0:17:14
 0:30:08
0:30:08
 0:59:51
0:59:51
 0:11:33
0:11:33
 0:08:38
0:08:38
 0:10:32
0:10:32
 0:16:50
0:16:50
 0:14:47
0:14:47
 0:29:35
0:29:35
 0:03:39
0:03:39
 0:00:25
0:00:25