filmov
tv
Differential Geometry: The Intrinsic Point of View #SoME3

Показать описание
#SoME3
Chapters:
0:00 Intro
2:19 How much does a curve ... curve?
3:56 Gaussian Curvature
7:14 Local Isometries
7:38 The Punchline
8:25 Intrinsic vs. Extrinsic
9:40 How does this apply to us?
By explaining the contents of Gauss' Theorema Egregium, I provide an overview of the "intrinsic point of view" in differential geometry: that is, from the point of view of living on a surface (or a manifold, more generally). I compare this point of view to that of a flatlander. Ultimately, this point of view applies more to our existence than we may think...
Chapters:
0:00 Intro
2:19 How much does a curve ... curve?
3:56 Gaussian Curvature
7:14 Local Isometries
7:38 The Punchline
8:25 Intrinsic vs. Extrinsic
9:40 How does this apply to us?
By explaining the contents of Gauss' Theorema Egregium, I provide an overview of the "intrinsic point of view" in differential geometry: that is, from the point of view of living on a surface (or a manifold, more generally). I compare this point of view to that of a flatlander. Ultimately, this point of view applies more to our existence than we may think...
Differential Geometry: The Intrinsic Point of View #SoME3
The clever way curvature is described in math
Differential Geometry in Under 15 Minutes
8 - Intrinsic Coordinates
Differential Geometry - 1 - Curves x Definitions and Technicalities
Lecture 9: Intrinsic Geometry of Surfaces
Differential Geometry, Bs Math-v ,Intrinsic Equation of a Curve
Geometry of space curve: intrinsic derivative and curvilinear coordinate system in space (MAT)
Differential Geometry: local isometries preserve intrinsic geometry, 4-7-21 part 5
Differential Geometry | Math History | NJ Wildberger
A Visual Intro to Curves and the Frenet Frame
Curvature on surface: intrinsic geometry of curves on surface-2 (MAT)
Differential Geometry #2 - Intrinsic, Extrinsic curvature, and other curvatures
Differential Geometry - 11 - Gauss Map x Gauss Curvature
Gauss, normals and fundamental forms | Differential Geometry 34 | NJ Wildberger
Curvature: Intuition and Derivation | Differential Geometry
An introduction to surfaces | Differential Geometry 21 | NJ Wildberger
Differential Forms: PART 1A: TANGENT SPACES (INTUITIVELY)
Lecture 5: Differential Forms (Discrete Differential Geometry)
Lecture 12: Smooth Surfaces I (Discrete Differential Geometry)
Differential Geometry - 9 - Surfaces x Charts
Lecture 20: Geodesics (Discrete Differential Geometry)
Differential geometry msc mathematics | Differential geometry | How to learn differential geometry
Lecture 1: Overview (Discrete Differential Geometry)
Комментарии
 0:11:13
0:11:13
 0:16:17
0:16:17
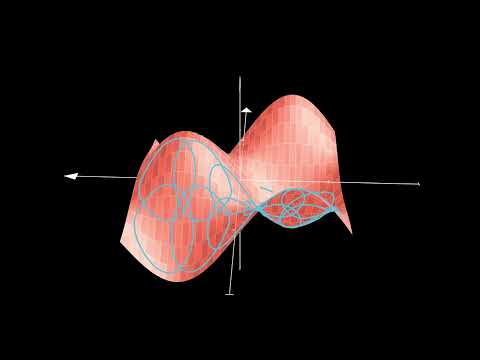 0:13:37
0:13:37
 0:12:52
0:12:52
 0:06:46
0:06:46
 1:14:55
1:14:55
 0:15:31
0:15:31
 0:25:08
0:25:08
 0:37:40
0:37:40
 0:51:32
0:51:32
 0:18:12
0:18:12
 0:23:59
0:23:59
 0:19:26
0:19:26
 0:10:49
0:10:49
 0:51:27
0:51:27
 0:08:34
0:08:34
 0:42:44
0:42:44
 0:05:43
0:05:43
 0:45:20
0:45:20
 1:20:43
1:20:43
 0:08:44
0:08:44
 1:55:24
1:55:24
 0:38:19
0:38:19
 1:07:46
1:07:46