Related Rates - The Shadow Problem

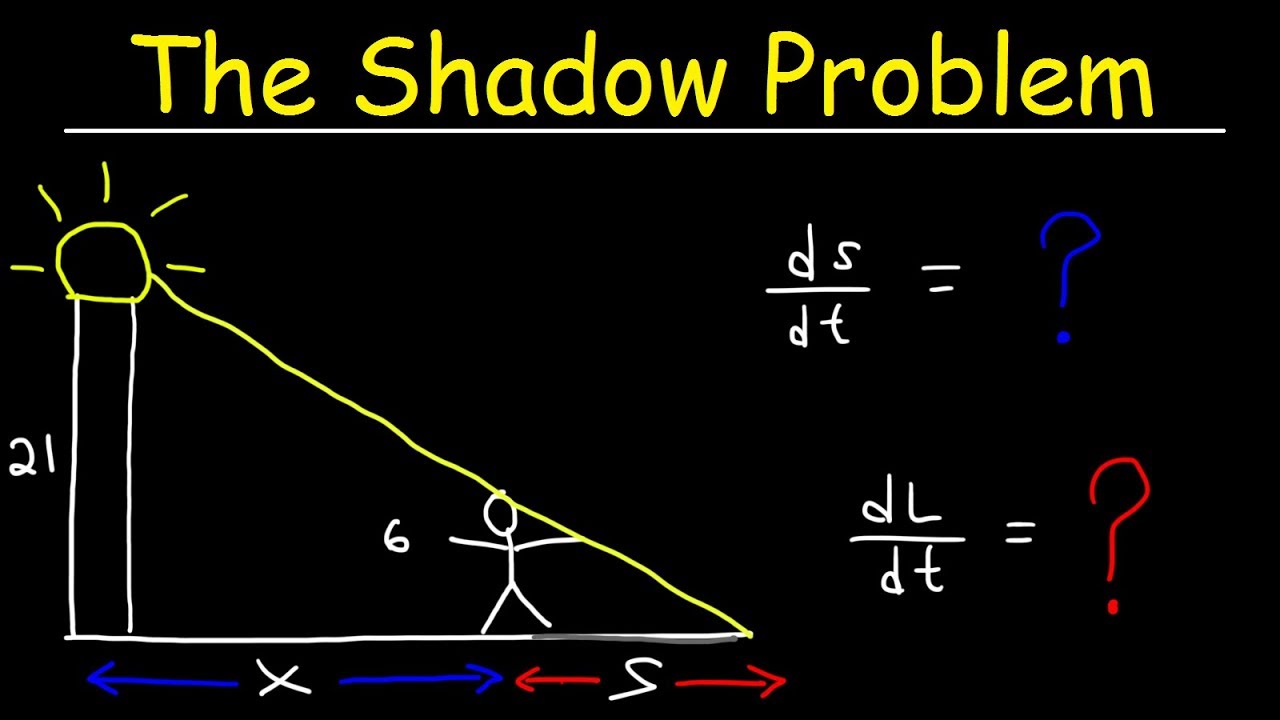
This calculus video tutorial explains how to solve the shadow problem in related rates. A 6ft man walks away from a street light that is 21 feet above the ground at a rate of 3ft/s. At what rate is the length of the shadow changing?

Introduction to Limits:

Derivatives - Fast Review:

Introduction to Related Rates:

Derivative Notations:

Related Rates - The Cube:

__________________________________
Inflated Balloon & Melting Snowball:

Gravel Dumped Into Conical Tank:

Related Rates - Area of a Triangle:

Related Rates - The Ladder Problem:

Related Rates - The Distance Problem:

____________________________________
Related Rates - Airplane Problems:

Related Rates - The Shadow Problem:

Related Rates - The Baseball Diamond Problem:

Related Rates - The Angle of Elevation Problem:

Related Rates - More Practice Problems:

_________________________________
Final Exams and Video Playlists:

Full-Length Videos and Worksheets:

[liezyldavila]

for those who are asking why 8ft from the street light is not included in part a. it turns out that as long as the man is moving at a constant rate, the rate of his shadow will also remain constant at 6/5 ft/sec. regardless of how
far away he is from the street light.

[shrmpy]

Bruh I learn more from u in 10 minutes than I do from my teacher in 10 classes. TYSM

[JonathanBrown-emboldened]

5 years later and you are still saving lives!

[ptyptypty]

for what it's worth.. the the rate at which the tip of the shadow is moving is equal to the Given velocity of the man walking PLUS the rate at which the shadow is moving. So, dx/dt + ds/dt is all you need. NO need to calculate using dL/dt. This was an extra step that was worthwhile to see. It's always good to see extra steps to learn as much about how a problem can be solved. GREAT VIDEO as USUAL.. You're the best!!! thanks for all the effort you've invested in all your videos...

[merkov]

I can't even believe I am now capable of solving these type of problems on my own. Thanks a lot man.

[hansonji]

everytime I face a difficult problem in calculus, your always here for me. Your the real MVP

[gabriel]

How do you know math so well? And how are you able to teach is so well? I've watched several of your videos and found each one very helpful. Thank you! I also comment and like every video of yours I watched, you know, for the youtube algorithm, but your videos are always the first to pop up, so I guess I am doing it because I really appreciate what you do.

[georgesadler]

MR. Organic Chemistry Tutor, this is another solid explanation of Shadow Problems in the Related Rates section of Calculus One. Calculus has some great Related Rates problem in its library. This is an error free video/lecture on YouTube TV with the Organic Chemistry Tutor.

[sin_]

For those wondering, dL/dt is enough to calculate everything. If we find how fast the tip of the shadow is changing, we can just extract 3 ft/s (because shadow gets smaller from that side) to find ds/dt.

[PushedInsanityYT]

Thanks a lot....i wasn't able to solve the first part by myself, but after understanding it, i was able to solve the second part by myself :) Whenever you guys solve these related rates problems, your first step should be to make a diagram and find an equation which relates both the variables which are changing w.r.t time! Good Luck :)

[MichaelSmith-nciy]

Great video and explanation. After this video, setting up and working out this type of problem made a lot more sense. The only question I have, which is more for a deeper understanding is why are the two "distances from the light" (8 ft for part A and 10 ft for part B) irrelevant?

[joecrow]

As a math tutor, I have been looking around for this concept. It is nice to see it here

[darthTwin]

I haven’t seen anyone put this yet, so I will. A simpler process can be used to ascertain the rate of the movement of the shadow tip:

Bc the length, L is the sum of x and s. dL/dt, the rate of change of the length with respect to time is the sum of the rates of s and x with respect to time.
L = s+x ->differentiate-> dL/dt = ds/dt + dx/dt (rule: derivative of sum is sum of derivatives)

This makes more sense to use bc after completing part A, we already have both components of this sum, dx/dt and ds/dt. This sum is 3 + 6/5 or 21/5.

It’s a faster method bc you simply compute one sum.

Lastly, I want to make it clear why the derivative of the entire length of the shape created tells us this (or at least my reasoning). The lamppost is a fixed point, so the combined length is dependent on the position of the shadow tip. Focusing just on the shadow tip and the lamppost, as the tip moves, the length expands.
Thus, finding the rate of change of the length gives the rate of movement of this tip.

[bluefire]

Amazing insight. Randomely encountered a similar problem and had no clue what to do. Thank you so much.

[victornnah]

This man is GOATED. I like the formula he used here, it just makes everything look easy. 🙏🔝

[Nathanator]

Got an exam in 15 minutes, this video was more helpful than my teacher’s lessons, thank you

[BooleansLab]

Genius. God bless you sir. Thank you for existing 🎉

[Kasleryoutube]

Beautiful, you’re so good at explaining

[LiveGoodPhilippines]

Thank you bro . You are so precise in explaining . Your way of explanation is way to good for us people who is not really good in direct solving. Thank you for explaining it step by step. 👍👆

[joshuayoo]

You teach these things like a GOD, you really deserve ur subscribers. In fact, I'm gonna sub right now!