filmov
tv
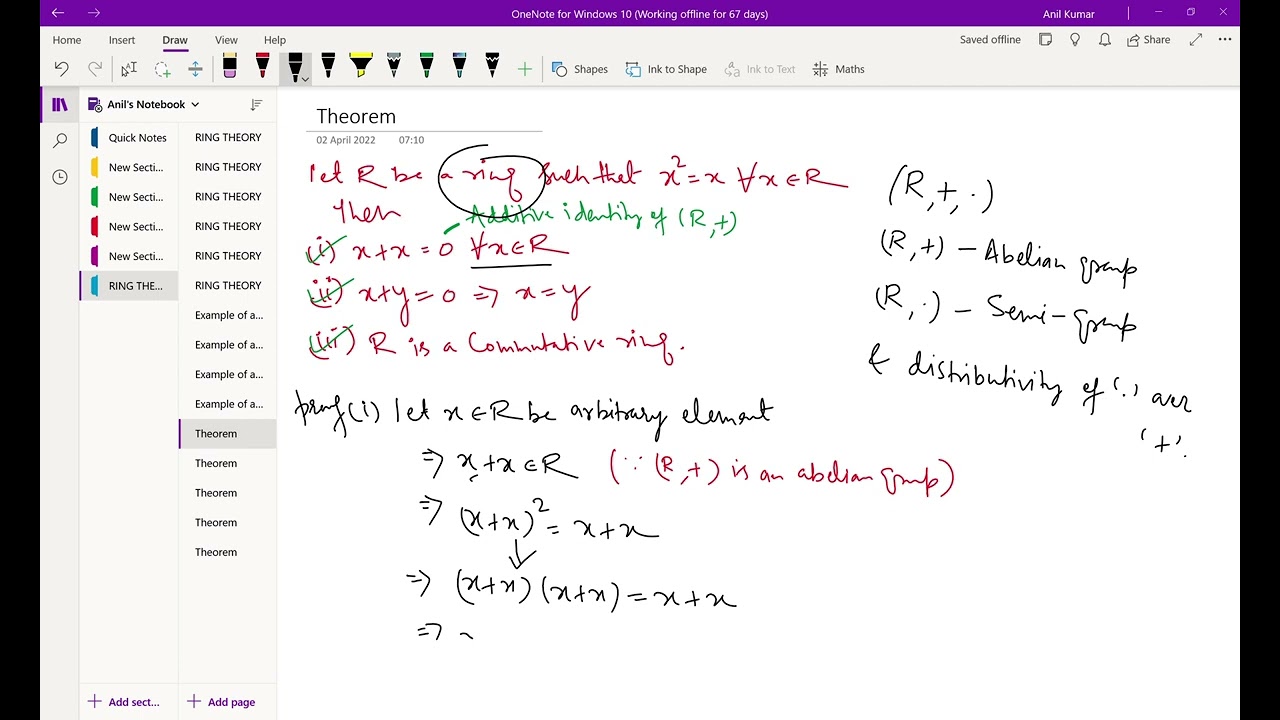
Prove that the ring R is commutative if x^2=x for all x in R.
Показать описание
Subscribe to my channel.
Share and like my video if you like the content.
#spreadlove
#nohate
Share and like my video if you like the content.
#spreadlove
#nohate
0:08:50
Prove a(-b) = -(ab) in Ring Theory
0:03:28
A Ring is Commutative iff (a - b)(a + b) = a^2 - b^2 Proof
0:22:23
Prove that if in a ring R, x^3=x for all x in R, then ring R is commutative.
0:18:01
Prove that the ring R is commutative if x^2=x for all x in R.
0:07:14
Units in a Ring (Abstract Algebra)
0:10:00
Abstract Algebra | The characteristic of a ring.
0:03:46
Prove that a ring R is commutative, if and only if (a+b)2 = a2 + 2ab + b2 | Jayesh Umre
0:07:18
Ring Examples (Abstract Algebra)
0:02:58
Every Boolean Ring is Commutative Proof
0:23:42
Algebraic Structures: Groups, Rings, and Fields
0:03:40
|| Ring || Show that a ring R is commutative iff (a+b)^2 =a^2+2ab+b^2
0:05:40
|| Ring ||Prove that a ring R is without zero divisor iff the cancellation law be hold in R.
0:02:35
Every Boolean Ring is of Characteristic 2 Proof
0:33:43
M is a maximal ideal of a ring R if and only if R/M is a field. Lecture 12.
0:11:04
Properties of Ring - Ring Theory - Algebra
0:22:49
Abstract Algebra | Units and zero divisors of a ring.
0:14:30
Abstract Algebra | Principal Ideals of a Ring
0:06:24
If R is a ring such that a^2=a then prove that)a+a=0()if a+b=0 then a=b(3) R is a commutative ring
0:08:25
Abstract Algebra 13.4: A Polynomial Factor Ring
0:24:58
Ring Theory LEC 10 || Ideal of Ring | prove that the set R[x] of polynomials over a ring R w.r.t to
0:05:15
Ring Theory IDEAL SURPRISES!! If 1 ∈ A, then A = R?!? If unit ∈ A, then A = R?!?
0:06:38
An ideal I of Commutative Ring with unity R is prime if and only if R/I is Integral Domain
0:06:31
Every Boolean Ring is Commutative Ring
0:17:06
Introduction to Ring, Field and Integral Domain - Algebraic Structures - Discrete Mathematics
Комментарии