Kuhn Tucker Optimality Conditions with inequality constraints. #KuhnTuckerConditions

the Karush–Kuhn–Tucker (KKT) conditions, also known as the Kuhn–Tucker conditions, are first derivative tests (sometimes called first-order necessary conditions) for a solution in nonlinear programming to be optimal, provided that some regularity conditions are satisfied.

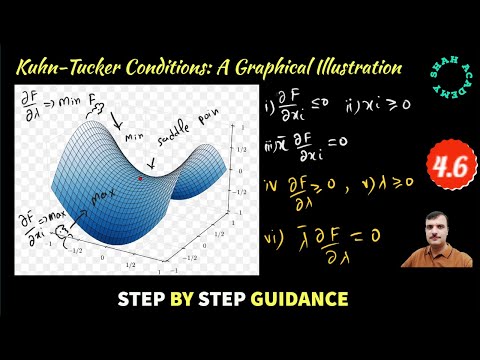
Allowing inequality constraints, the KKT approach to nonlinear programming generalizes the method of Lagrange multipliers, which allows only equality constraints. Similar to the Lagrange approach, the constrained maximization (minimization) problem is rewritten as a Lagrange function whose optimal point is a saddle point, i.e. a global maximum (minimum) over the domain of the choice variables and a global minimum (maximum) over the multipliers, which is why the Karush–Kuhn–Tucker theorem is sometimes referred to as the saddle-point theorem.
Consider the case of a two-good world where both goods, x and y. are rationed. Let the consumer’s utility function be U = U(x,y). The consumer has a fixed money budget of B and faces the money prices Px and Py. Further, the consumer has an allotment of coupons, denoted C, which can be used to purchase both x or y at a coupon price of cx and cy. Therefore the consumer’s maximization problem is Maximize U =U(x,y) Subject to and B ≥Pxx+Pyy C ≥cxx+cyy in addition, the non-negativity constraint x ≥ 0 and y ≥ 0. The Lagrangian for the problem is Z =U(x,y)+λ(B−Pxx−Pyy)+λ2(C −cxx+cyy) where λ,λ2 are the Lagrange multiplier on the budget and coupon constraints respectively. The Kuhn-Tucker conditions are Zx =Ux−λ1Px−λ2cx =0 Zy =Uy −λ1Py −λ2cy =0 Zλ1 = B−Pxx−Pyy ≥0 λ1≥0 Zλ2 = C −cxx−cyy ≥0 λ2≥0 Numerical Example Let’s suppose the utility function is of the form U = x · y2. Further, let B =100,Px = Py =1while C =120and cx =2,cy =1. The Lagrangian becomes Z =xy2+λ1(100−x−y)+λ2(120−2x−y) The Kuhn-Tucker conditions are now Zx =y2 −λ1−2λ2 ≤0 x≥0 x·Zx=0 Zy =2xy−λ1−λ2 ≤0 y ≥0 y·Zy =0 Zλ1 =100−x−y ≥0 λ1 ≥0 λ1·Zλ1 =0 Zλ2 =120−2x−y ≥0 λ2 ≥0 λ2·Zλ2 =0

[ECONMATHS]

Make sure you like comment and share this channel with your friends

[GretgorPooper]

Just dropped by to say you saved my life back in college. Indian guys on youtube are a blessing.

[---nurv]

Such an amazing video! you explained it so much better than any other video I watched (and my teachers)!

[tariqislam]

One of the best videos on KKT conditions. Thank you!!

[selamidurmus]

The rooster is also learning the Karush–Kuhn–Tucker conditions :D

[ykdzzn]

Thank you so much for this video. It really helped me for our examination tomorrow.

[蒼井なつこ]

u rescued me from my math in econ exam. Thanks and please keep doing these videos ! They are really helpful

[mantrikashukla]

this was so so helpful and clearly explained! thank you

[thotyashimray]

This is gonna help IGNOU MEC students a lot

[laminbsanyang]

Wonderful explanation resulting in wonderful understanding...
Thank you, sir...

[merin_here_am_i]

Keep up the good work. The video content was very useful.

[greenfairyfloss]

best kuhn-tucker explainer video on YouTube!!!

[kaylashevadena]

Thankkk you u helping me understand it very well 🙏🏻

[temamuna]

This is amazing! Clearly and well explained.Thank you sir.

[johnmefful]

Thank you very much
you have been very helpful

[tjaloismtowa]

My professor need to subscribe to your channel man, I understood you better than the professor or even my friend who tried explaining it after

[shubhranshuranjandas]

sir, please make a video on projected gradient method and quadratic programming method

[mightym]

Thank you so much... from Ethiopia!
Just one more thing, you also need to put both lambda 1 and 2 to be greater than zero, which means checking if both constraints work.

Thanks

[ArmanAli-wwml]

So what are those 4 conditions? Please explain each

[chrismashau]

Can you cover the principal agent problem in information economics