filmov
tv
Jordan Canonical Form

Показать описание
In this video I calculate the Jordan canonical form of a 3x3 matrix by presenting all the 3 cases that could occur. This approach is a bit nontraditional and is a bit longer than the usual approach, but it works most of the time is (in my opinion) easier to apply. A similar approach works for matrices of larger size. Enjoy!
Update: I got an e-mail about this, and it turns out that this approach only works if and only if you can solve the equations that I gave you, which should be most of the time anyway. An example where it doesn't work is for example the matrix A = [1 1/2 1/2; 0 1/2 -1/2; 0 1/2 3/2]. For that matrix, you'd have to revert to the classical approach of finding the Jordan Canonical Form.
Update: I got an e-mail about this, and it turns out that this approach only works if and only if you can solve the equations that I gave you, which should be most of the time anyway. An example where it doesn't work is for example the matrix A = [1 1/2 1/2; 0 1/2 -1/2; 0 1/2 3/2]. For that matrix, you'd have to revert to the classical approach of finding the Jordan Canonical Form.
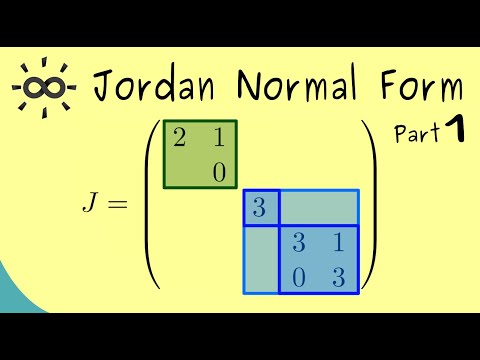
Jordan Normal Form 1 | Overview
Introduction to Jordan Canonical Form
Jordan Canonical Form
Systems of Differential Equations: Diagonalization and Jordan Canonical Form
The Jordan Form of a 3 by 3 matrix: Example 1
Determining the Jordan canonical form - example 1
Jordan Canonical Form of a 3x3 Matrix
Example of Jordan Canonical Form: Real 4x4 Matrix with Basis 1
Example of Jordan Canonical Form: 2x2 Matrix
Jordan canonical form
LAII 009 Example of a Jordan normal form
Examples On Diagonal Canonical Form & Jordan Canonical Form | GATE Control System
Jordan Canonical Form of 4 by 4 Matrix
Advanced Linear Algebra 25: Jordan Decomposition Generalized Eigenspace
Jordan canonical form Minimal Polynomial linear algebra Characteristic Polynomial of Matrices
Advanced Linear Algebra 24: Finding Blocks of Jordan Decomposition
Jordan canonical form |How to get JC form of a matrix |(part-1)
Conversion of Transfer Function into Jordan Canonical form - Control Systems State Space Analysis
Jordan canonical form with example| EEE
Lecture 29 : Minimal Polynomial and Jordan Canonical Form-I
Generalized Eigenvectors and Jordan Canonical Form
Linear Algebra 22: Convert a 3x3 matrix into Jordan form (Ch10 Pr2c)
Jordan Normalform, Übersicht mit Diagonalmatrix, Lineare Algebra | Mathe by Daniel Jung
CSIR NET MATHEMATICS| Linear Algebra | How to Calculate Jordan Canonical Form? (June 2018)
Комментарии
 0:14:59
0:14:59
 0:22:10
0:22:10
 0:23:25
0:23:25
 0:34:25
0:34:25
 0:10:28
0:10:28
 0:05:47
0:05:47
 0:10:24
0:10:24
 0:05:24
0:05:24
 0:10:20
0:10:20
 0:20:41
0:20:41
 0:06:33
0:06:33
 0:37:29
0:37:29
 0:12:09
0:12:09
 0:47:14
0:47:14
 0:05:55
0:05:55
 0:45:22
0:45:22
 0:14:09
0:14:09
 0:15:06
0:15:06
 0:07:05
0:07:05
 0:31:00
0:31:00
 0:37:43
0:37:43
 0:08:41
0:08:41
 0:05:29
0:05:29
 0:09:39
0:09:39