filmov
tv
10 - Series and Sigma Summation Notation - Part 1 (Geometric Series & Infinite Series)

Показать описание
In this lesson, you will learn what a series is in math and how they compare to sequences. A series is the sum of the terms of a sequence. We have already discussed some special sequences such as the arithmetic sequence and geometric sequence. We now extend this idea and discuss the arithmetic and geometric series, infinite series, finite series, and more. We also spend a great deal of time introducing the sigma notation for summation, which is how we actually write the series down when solving problems..
10 - Series and Sigma Summation Notation - Part 1 (Geometric Series & Infinite Series)
Sigma Notation and Summation Notation
what is sigma notation and how to we use it
Writing arithmetic series in sigma notation
Sigma notation for sums | Sequences, series and induction | Precalculus | Khan Academy
Summation Formulas and Sigma Notation - Calculus
Sigma characters that are good, pure evil or broken (part 2)
Fake sigma vs real sigma #shorts #viral #fyp #sigma
Sigma FP BIT DEPTH Deep Dive
Sigma Notation or Summation Notation | Sequence and Series
How to write the rule of a sum in sigma notation
Putin flirts, Putin sigma rule, Putin body language #sigma #confidence #bodylanguage #putin #shorts
Sigma x Beast
Anime Sigma Males 🔥#shorts #animeedit #sigma #sigmamale
Express Each Geometric Series In Sigma Notation And Find Sum 1- 2 + 4 - 8 +16-32
Evaluate Sum of 3i - 10 Finite Series with Sigma Notation | Grade 11 | IITJEE
One of the best climax #sigma
Arithmetic Sequences and Arithmetic Series - Basic Introduction
Sigma notation practice example
Geometric Series | Sigma Notation
Determine the Partial Sum of an Arithmetic Series Given in Sigma Notation
Sigma (Summation) Notation # #algebra #summation #sigmanotation
Evaluate Sum of Series with Sigma Notation Higher Lower Limit | Grade 11 | IITJEE
SIGMA REJECTS PLUS SIZED GIRLS #shorts #sigma #thebutton
Комментарии
 0:31:04
0:31:04
 0:15:41
0:15:41
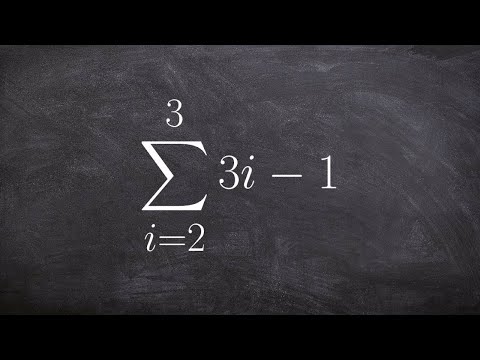 0:01:22
0:01:22
 0:04:07
0:04:07
 0:04:27
0:04:27
 0:20:24
0:20:24
 0:00:24
0:00:24
 0:00:14
0:00:14
 0:12:12
0:12:12
 0:11:01
0:11:01
 0:04:18
0:04:18
 0:00:20
0:00:20
 0:00:13
0:00:13
 0:00:13
0:00:13
 0:03:41
0:03:41
 0:05:26
0:05:26
 0:00:30
0:00:30
 0:44:04
0:44:04
 0:03:23
0:03:23
 0:04:31
0:04:31
 0:04:17
0:04:17
 0:00:51
0:00:51
 0:05:16
0:05:16
 0:00:47
0:00:47