filmov
tv
how floating point works
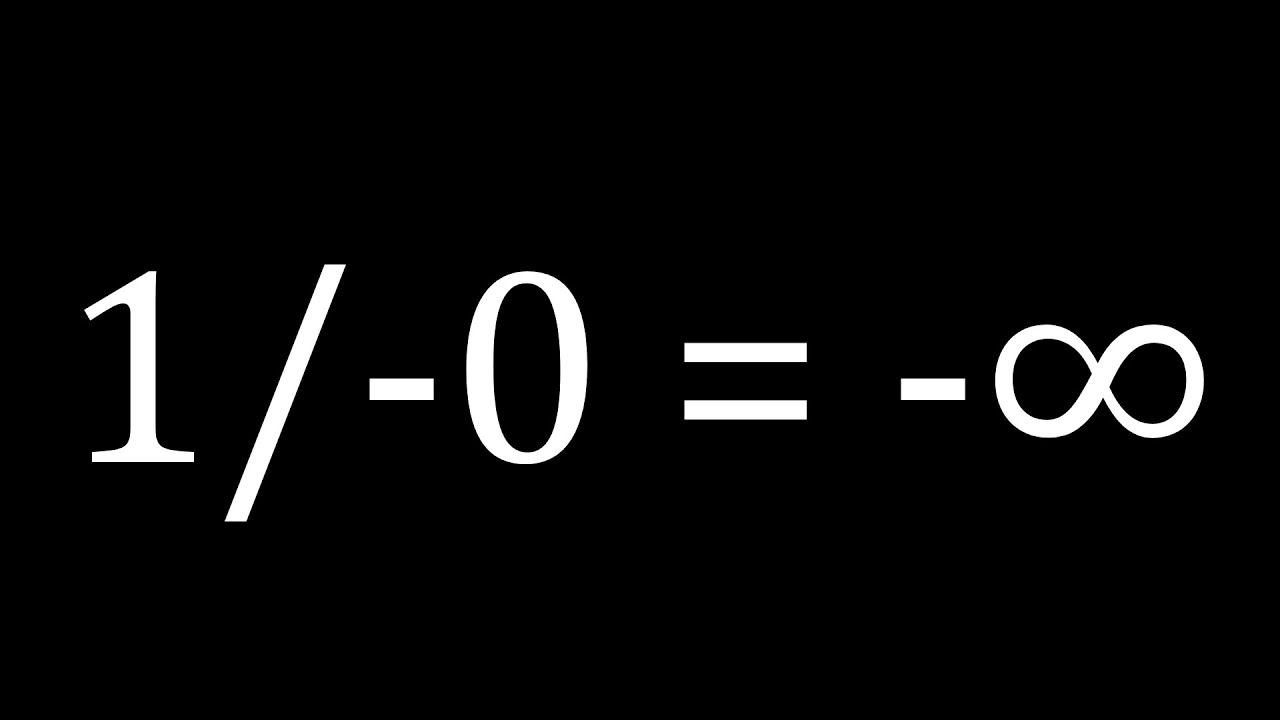
Показать описание
a description of the IEEE single-precision floating point standard
how floating point works
Floating Point Numbers - Computerphile
How do Floating Point Numbers Work?
How Floating Point Numbers Work (in 7 minutes!)
Why Is This Happening?! Floating Point Approximation
Wait, so comparisons in floating point only just KINDA work? What DOES work?
What is Floating-Point Performance?
Floating Point Numbers (Part1: Fp vs Fixed) - Computerphile
Binary 4 – Floating Point Binary Fractions 1
Representations of Floating Point Numbers
Floating Point Numbers
IEEE 754 Standard for Floating Point Binary Arithmetic
Floating Point Numbers | Fixed Point Number vs Floating Point Numbers
An Introduction To Floating Point Math - Martin Hořeňovský - NDC TechTown 2022
Lecture 19. Floating-Point Unit (FPU)
Floating Point Numbers
Why Computers Screw up Floating Point Math
How the FPU works #1 Explaining Floating Point
Why computers can't add up. Floating Point Arithmetic.
Decimal to IEEE 754 Floating Point Representation
Math for Game Developers - Floating Point Numbers
CppCon 2015: John Farrier “Demystifying Floating Point'
Floating Point Numbers (Part2: Fp Addition) - Computerphile
Floating Point Number Representation IEEE-754 ~ C Programming
Комментарии
 0:17:48
0:17:48
 0:09:16
0:09:16
 0:03:27
0:03:27
 0:06:44
0:06:44
 0:05:46
0:05:46
 0:15:41
0:15:41
 0:04:43
0:04:43
 0:15:41
0:15:41
 0:11:20
0:11:20
 0:13:50
0:13:50
 0:12:32
0:12:32
 0:21:34
0:21:34
 0:13:40
0:13:40
 0:45:24
0:45:24
 0:15:04
0:15:04
 0:17:30
0:17:30
 0:12:10
0:12:10
 0:22:06
0:22:06
 0:04:29
0:04:29
 0:09:27
0:09:27
 0:09:43
0:09:43
 0:47:34
0:47:34
 0:08:09
0:08:09
 0:05:15
0:05:15