filmov
tv
Wait, so comparisons in floating point only just KINDA work? What DOES work?

Показать описание
An introduction to the floating point numbers (iee-754), and some of the oddities surrounding it.
Disclaimer: Commission is earned from qualifying purchases on Amazon links.
Follow me on:
Some great resources:
Some more great stuff:
Disclaimer: Commission is earned from qualifying purchases on Amazon links.
Follow me on:
Some great resources:
Some more great stuff:
Wait, so comparisons in floating point only just KINDA work? What DOES work?
Why Is This Happening?! Floating Point Approximation
How (not) to compare floating-point numbers
Float vs int in java. #java #tutorial #float #int #shibainu #doge #meme
C++ How To Check If Floating Point Numbers Are Nearly The Same
42 - How to compare floating point numbers in c++
how floating point works
ChatGPT, Compare Two Float Numbers
Your Twelfth Day in C (Floating Point Comparison) - Crash Course in C Programming
6.2 Comparing floating-point numbers for equality
Who Broke JavaScript Floating Point Numbers? [Intermediate Tutorial]
C++ : Floating point comparison precision
Why 0.1 + 0.2 is not 0.3? | Floating point errors #shorts
Why computers can't add up. Floating Point Arithmetic.
JavaScript Handling Floating Point Values #shorts #javascript #programming #coding
Floating Point Comparison Problem || Laravel || PHP
rounding - How to round float numbers in javascript?
floating point - How to parse float with two decimal places in javascript?
Floating Point Leviathan (HD trailer)
Floating Point Numbers - Theory and Practice
C# : How deterministic is floating point inaccuracy?
8. Visualizing the Floating Point Format - Audio Number Formats
Visualizing Floating Point Imprecision
ICC 2023 - Change a Bit to save Bytes: Compression for Floating Point Time-Series Data [WITH AUDIO]
Комментарии
 0:15:41
0:15:41
 0:05:46
0:05:46
 0:03:59
0:03:59
 0:00:06
0:00:06
 0:07:15
0:07:15
 0:02:20
0:02:20
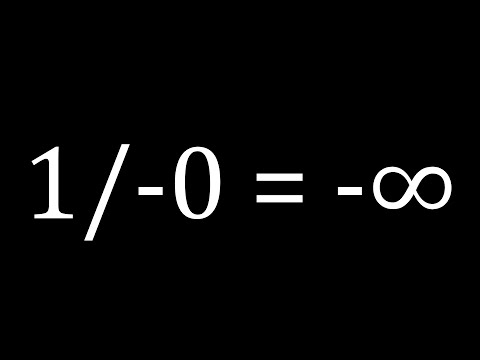 0:17:48
0:17:48
 0:03:52
0:03:52
 0:08:16
0:08:16
 0:09:08
0:09:08
 0:19:52
0:19:52
 0:01:34
0:01:34
 0:00:54
0:00:54
 0:04:29
0:04:29
 0:00:26
0:00:26
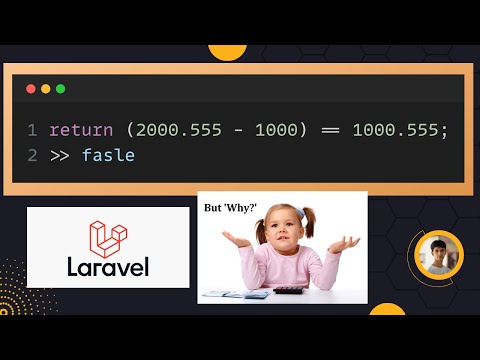 0:02:30
0:02:30
 0:00:27
0:00:27
 0:00:26
0:00:26
 0:00:35
0:00:35
 1:03:25
1:03:25
 0:01:07
0:01:07
 0:10:34
0:10:34
 0:02:04
0:02:04
 0:06:10
0:06:10