filmov
tv
Why do colliding blocks compute pi?

Показать описание
An equally valuable form of support is to simply share some of the videos.
Many of you shared solutions, attempts, and simulations with me this last week. I loved it! You all are the best. Here are just two of my favorites.
NY Times blog post about this problem:
The original paper by Gregory Galperin:
For anyone curious about if the tan(x) ≈ x approximation, being off by only a cubic error term, is actually close enough not to affect the final count, take a look at sections 9 and 10 of Galperin's paper. In short, it could break if there were some point where among the first 2N digits of pi, the last N of them were all 9's. This seems exceedingly unlikely, but it quite hard to disprove.
Although I found the approach shown in this video independently, after the fact I found that Gary Antonick, who wrote the Numberplay blog referenced above, was the first to solve it this way. In some ways, I think this is the most natural approach one might take given the problem statement, as corroborated by the fact that many solutions people sent my way in this last week had this flavor. The Galperin solution you will see in the next video, though, involves a wonderfully creative perspective.
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
Music by Vincent Rubinetti.
Download the music on Bandcamp:
Stream the music on Spotify:
Timestamps
0:00 - Recap on the puzzle
1:10 - Using conservation laws
6:55 - Counting hops in our diagram
11:55 - Small angle approximations
13:04 - Summary
Thanks to these viewers for their contributions to translations
German: Greenst0ne
Hebrew: Omer Tuchfeld
------------------
Various social media stuffs:
Many of you shared solutions, attempts, and simulations with me this last week. I loved it! You all are the best. Here are just two of my favorites.
NY Times blog post about this problem:
The original paper by Gregory Galperin:
For anyone curious about if the tan(x) ≈ x approximation, being off by only a cubic error term, is actually close enough not to affect the final count, take a look at sections 9 and 10 of Galperin's paper. In short, it could break if there were some point where among the first 2N digits of pi, the last N of them were all 9's. This seems exceedingly unlikely, but it quite hard to disprove.
Although I found the approach shown in this video independently, after the fact I found that Gary Antonick, who wrote the Numberplay blog referenced above, was the first to solve it this way. In some ways, I think this is the most natural approach one might take given the problem statement, as corroborated by the fact that many solutions people sent my way in this last week had this flavor. The Galperin solution you will see in the next video, though, involves a wonderfully creative perspective.
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.
Music by Vincent Rubinetti.
Download the music on Bandcamp:
Stream the music on Spotify:
Timestamps
0:00 - Recap on the puzzle
1:10 - Using conservation laws
6:55 - Counting hops in our diagram
11:55 - Small angle approximations
13:04 - Summary
Thanks to these viewers for their contributions to translations
German: Greenst0ne
Hebrew: Omer Tuchfeld
------------------
Various social media stuffs:
Комментарии
 0:15:16
0:15:16
 0:05:13
0:05:13
 0:14:41
0:14:41
 0:04:12
0:04:12
 0:00:12
0:00:12
 0:00:22
0:00:22
 0:06:43
0:06:43
 0:07:30
0:07:30
 0:10:37
0:10:37
 0:50:25
0:50:25
 0:02:27
0:02:27
 0:00:55
0:00:55
 0:00:13
0:00:13
 0:03:31
0:03:31
 0:03:49
0:03:49
 0:02:31
0:02:31
 0:05:14
0:05:14
 0:02:59
0:02:59
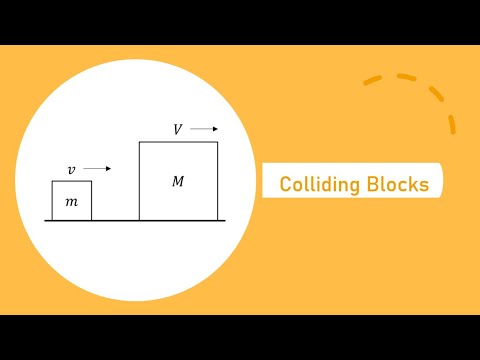 0:03:31
0:03:31
 0:31:42
0:31:42
 0:04:49
0:04:49
 0:11:23
0:11:23
 0:21:53
0:21:53
 0:00:29
0:00:29