filmov
tv
Multiplicative Inverse of 3 (mod 26)

Показать описание
How to use Euclid's Algorithm to find a multiplicative inverse of 3 (mod 26)
Multiplicative Inverse of 3 (mod 26)
Finding Modular Inverses
How To Find The Inverse of a Number ( mod n ) - Inverses of Modular Arithmetic - Example
Multiplicative inverses mod n
Multiplicative Inverse
Extended Euclidean Algorithm and Inverse Modulo Tutorial
Multiplicative Inverse (Modular) - Lesson 9 [Topics in Discrete Mathematics]
calculating the inverse of a number in some modulus for example inverse(11) mod 26=?
Modular inverse made easy
Mod - Inverses
How to find modular multiplicative inverses
The inverse of 3 modulo 7 is?
inverse modulo
Modular Multiplicative Inverse - Cryptography - Cyber Security - CSE4003
Two Easy Steps Of Modular Calculation.
How To Find Modular Multiplicative Inverses
Modular Additive & Multiplicative Inverse – 2 worked examples (video)
Modulo Operator Examples #Shorts #math #maths #mathematics #computerscience
Number Theory | Inverses modulo n
Extended Euclidean Algorithm using Example Multiplicative inverse of a number | Cryptography
Multiplicative inverses mod N
How to find out Multiplicative Inverse of any Number ? // 👍
Multiplicative inverse
2.2.3 Inverses mod n: Video
Комментарии
 0:07:36
0:07:36
 0:05:01
0:05:01
 0:10:58
0:10:58
 0:13:22
0:13:22
 0:10:03
0:10:03
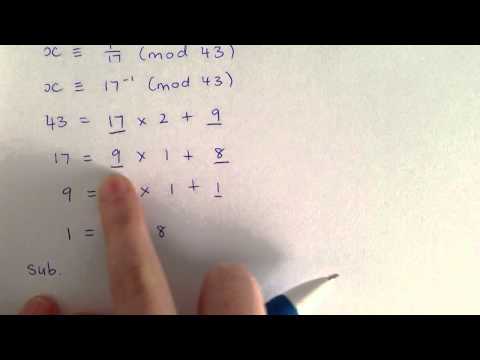 0:06:00
0:06:00
 0:06:20
0:06:20
 0:01:33
0:01:33
 0:04:12
0:04:12
 0:18:48
0:18:48
 0:04:20
0:04:20
 0:01:21
0:01:21
 0:00:15
0:00:15
 0:15:14
0:15:14
 0:00:32
0:00:32
 0:05:58
0:05:58
 0:05:02
0:05:02
 0:00:30
0:00:30
 0:08:02
0:08:02
 0:04:24
0:04:24
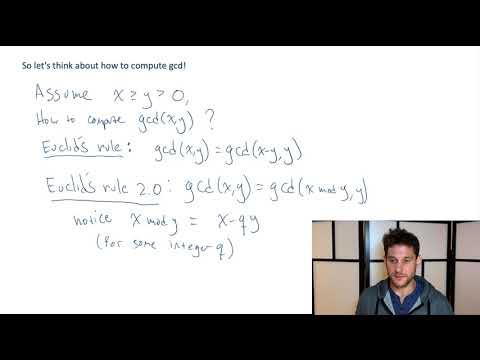 0:14:22
0:14:22
 0:00:23
0:00:23
 0:00:11
0:00:11
 0:04:17
0:04:17