filmov
tv
Finding a Basis for the Nullspace or Column space of a matrix A

Показать описание
Description: Two important subspaces associated to any matrix A are Null(A) and Col(A). We can look at the RREF form to quickly determine a basis for these subspaces
Learning Objectives:
1) Find a basis for Null(A) given a matrix A
2) Find a basis for Col(A) given a matrix A
This video is part of a Linear Algebra course taught at the University of Cincinnati.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Learning Objectives:
1) Find a basis for Null(A) given a matrix A
2) Find a basis for Col(A) given a matrix A
This video is part of a Linear Algebra course taught at the University of Cincinnati.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Basis and Dimension
Find a Basis for a Set of Vectors
Finding Basis for the Column Space of a Matrix | Linear Algebra
Basis and dimension
Basis and Dimension
Finding Basis for Column Space, Row Space, and Null Space - Linear Algebra
How to Find the Basis of a Subspace
Basis of a subspace | Vectors and spaces | Linear Algebra | Khan Academy
Finding safety solutions to Phoenix's perilous roadways
Finding Basis for the Row Space of a Matrix | Linear Algebra
How to Easily Find the Basis of the Span of Vectors - Linear Algebra
Independence, Basis, and Dimension
Finding a Basis for the Nullspace or Column space of a matrix A
Finding a basis for the column space
Finding a Basis for the Eigenspace of a Matrix
Linear Algebra: finding a basis for eigenspace 1/2
Find a basis for the span of a set of vectors (either a subspace or a vector space)
Change of Basis
Linear Algebra Example Problems - Basis for an Eigenspace
Null space and column space basis | Vectors and spaces | Linear Algebra | Khan Academy
Finding Basis of Kernel and Range of a Linear Transformation - Linear Algebra
Determine a Basis for the Kernel of a Matrix Transformation (3 by 4)
Check something is a basis
How to Find Eigenvalue and Basis for Eigenspace
Комментарии
 0:10:06
0:10:06
 0:07:17
0:07:17
 0:03:59
0:03:59
 0:06:20
0:06:20
 0:08:10
0:08:10
 0:18:31
0:18:31
 0:09:46
0:09:46
 0:19:00
0:19:00
 0:05:31
0:05:31
 0:01:59
0:01:59
 0:13:40
0:13:40
 0:13:20
0:13:20
 0:09:45
0:09:45
 0:09:05
0:09:05
 0:12:17
0:12:17
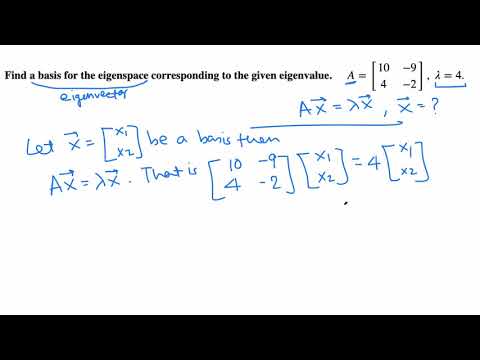 0:05:40
0:05:40
 0:08:56
0:08:56
 0:09:34
0:09:34
 0:07:48
0:07:48
 0:25:13
0:25:13
 0:20:19
0:20:19
 0:04:16
0:04:16
 0:03:53
0:03:53
 0:09:19
0:09:19